Understanding Minimax Algorithm with Tic Tac Toe
The Minimax algorithm is a type of backtracking algorithm used in Game Theory to determine the best move to make assuming your opponent is also making their best move. The use of Minimax algorithm is a form of Artificial Intelligence that does not involve Machine Learning. This article explains Minimax algorithm and explores how it can be used to determine the next move in a game of Tic Tac Toe.
Related articles on TDD in SwiftUI:
- Test Driven Development in SwiftUI - Part 1
- Test Driven Development in SwiftUI - Part 2
- Understanding Minimax Algorithm with Tic Tac Toe
- Test Driven Development in SwiftUI - Part 3
- Fixing a bug in Tic Tac Toe with TDD
Conditions in which MiniMax algorithm works
- Each player takes alternate moves
- Each player is playing optimally to win
- The game is strategic and is not reliant on any element of chance
Maximizing and Minimizing
To apply the minimax algorithm to a game, one player is assigned to be the maximising player and the other player is assigned to be the minimising player. The maximising player plays to try and get the highest possible score while the minimising player plays to get the lowest possible score. At every point in the game, the board can be evaluated to determine the current score. The maximising player wins if the final score is a positive result while the minimising player wins if the score is a negative result and the game is a draw if the result is zero.
Maximising player evaluates the best move to make knowing that their opponent will also make the best move that they can make. The next move is decided by creating a tree structure and evaluating each possible move alternating between the maximising and minimising players and calculating the score for the final outcome. To evaluate every single move in a game like chess is complicated and can be computationally very expensive, however in a game like Tic Tac Toe it is possible to evaluate every move.
In a single move, the Maximising player will always choose the path that yields the largest score.
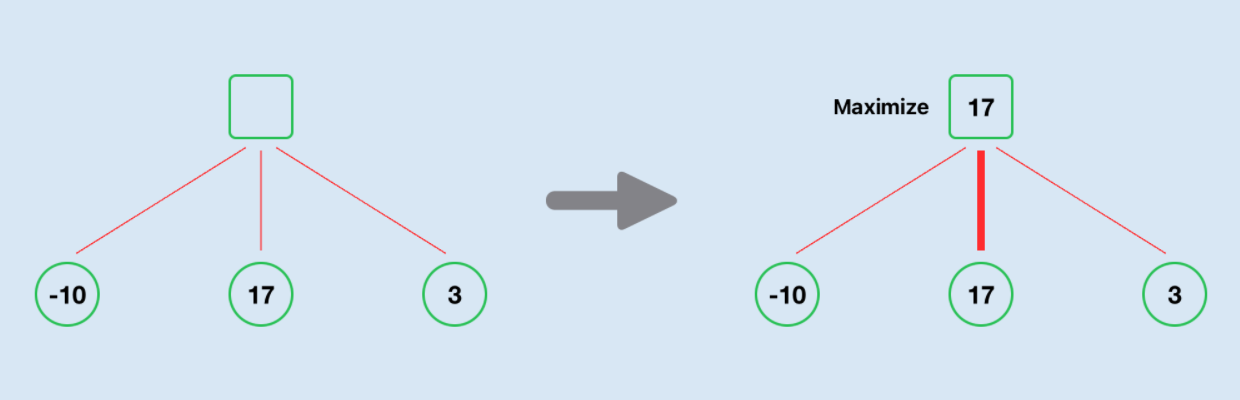
Maximise selects the move with the largest score
The Minimising player will always choose the path that yields the lowest score.
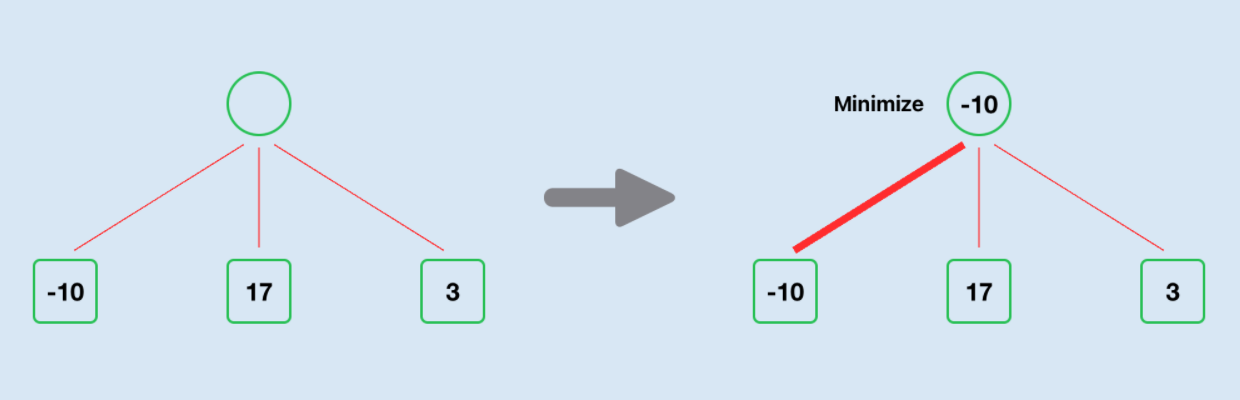
Minimise selects the move with the smallest score
Sample binary tree with four levels
A game will have multiple moves available to a player and there can be multiple turns remaining until the game is over. In chess for example, it is estimated that a player can have about 35 moves available to them at each turn. In tic tac toe, there are 9 available moves for the first player and 8 possible moves for the second player for each of the 9 opening moves.
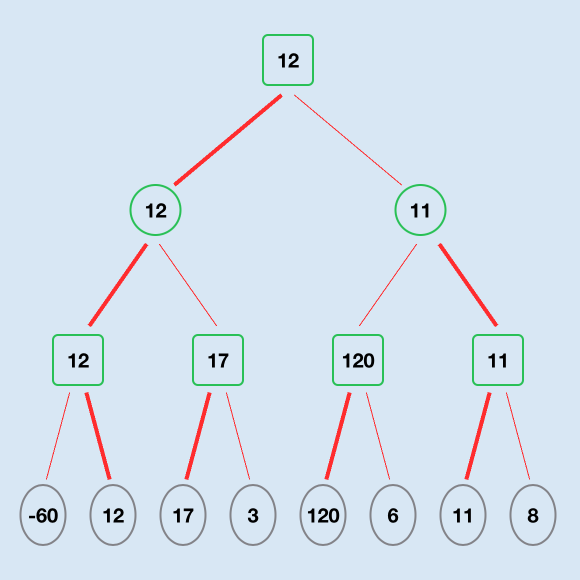
Let's take a hypothetical game where there are only two moves available to each player and given the set of random numbers representing the board evaluation after 4 moves. At each level the player has to choose between two possible paths. Assume it is the Maximising players turn. The Minimax algorithm will perform a depth-first traversal of all the paths to evaluate the best move.
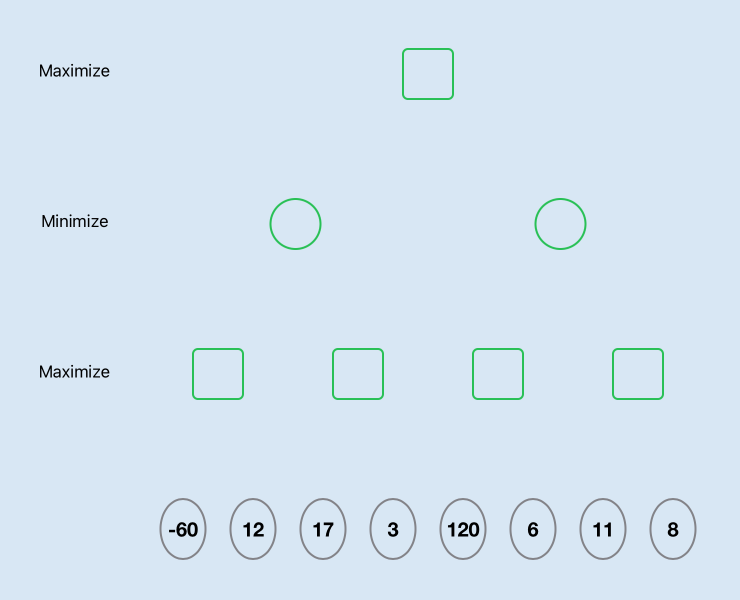
Sample results in a game with only two moves available
The maximising player will choose 12 between -60 and 12 and will choose 17 between 17 and 3. The minimising player will then choose 12 between 12 and 17.
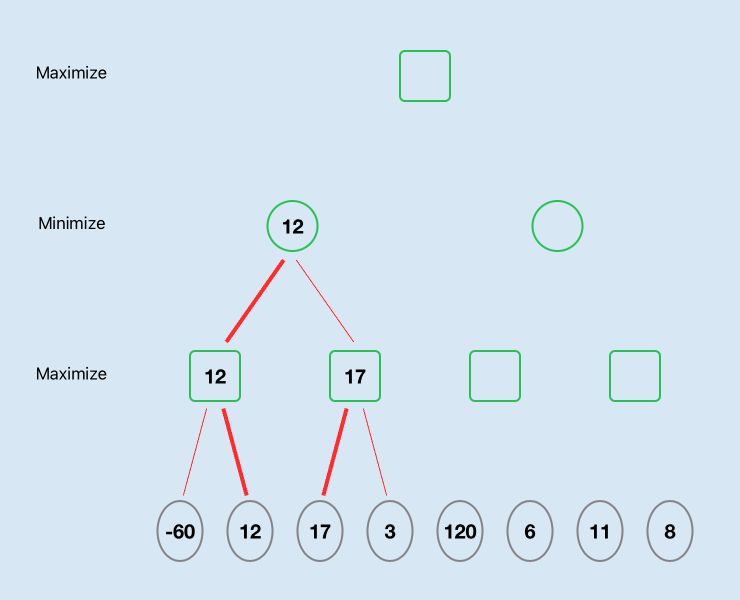
The left path resolves to a score of 12
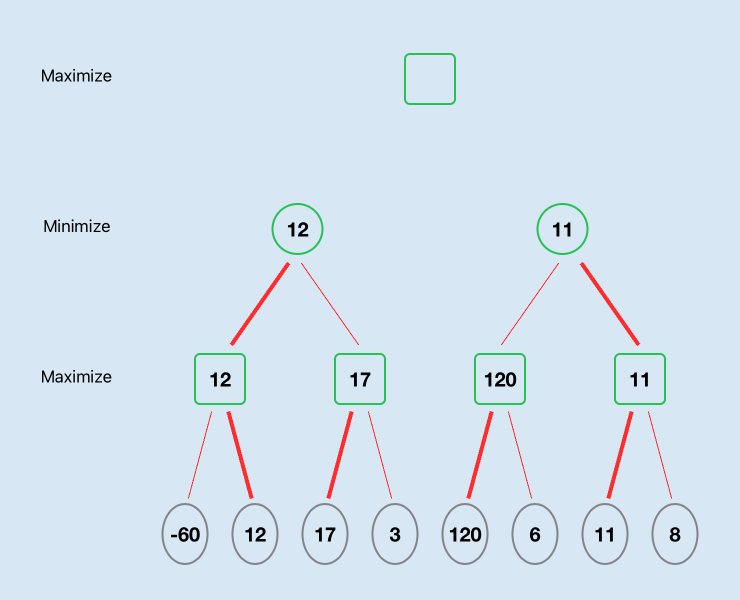
The left path resolves to a score of 11
So the best path for the maximising player to choose is the left path.
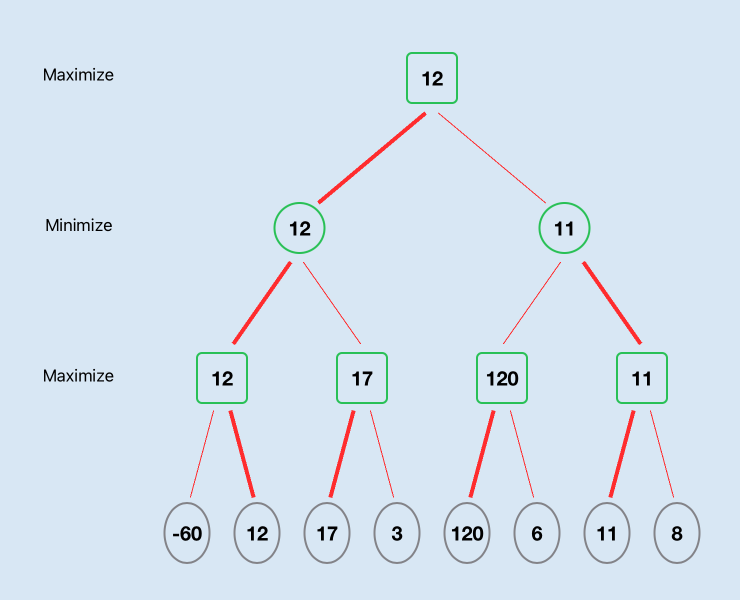
The best option for the Maximising player is the left path
Applying Minimax to Tic Tac Toe
To use Minimax in determine the best move to make in a game of Tic Tac Toe, we assign one player to be the Maximising player and the other to be the Minimising player.
Let's say X is the maximising player and O is the minimising player. One of the simplest scoring strategies would be to assign a value of plus 1 for a row containing 3 X tokens [X Wins] and a value of -1 for a row containing 3 O tokens [O Wins] and a value of zero when the game is a draw. The next move for current player can be evaluated by following a path for each possible move. Each player can predict that their opponent will equally make their best possible move. Player X is looking for a score of 1, while player O is looking for a score of -1.
This is a bit like
- "I know what you will do"
- "You know I know what you will do"
- "I know you know I know what you will do"
- and so on...
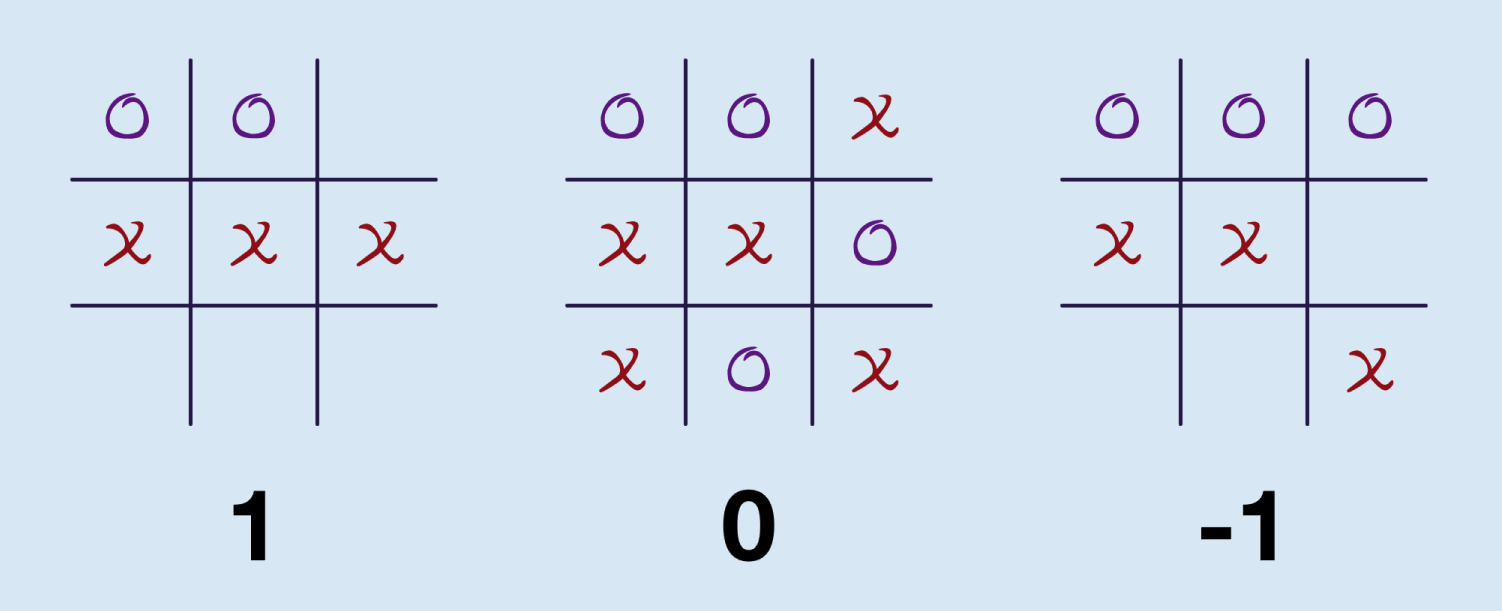
Minimax scores for tic tac toe with X as the maximising player
Sample next moves for Maximising player
Given the sample board below the minimax algorithm can be used to determine the best move for player X (the maximising player) to make.
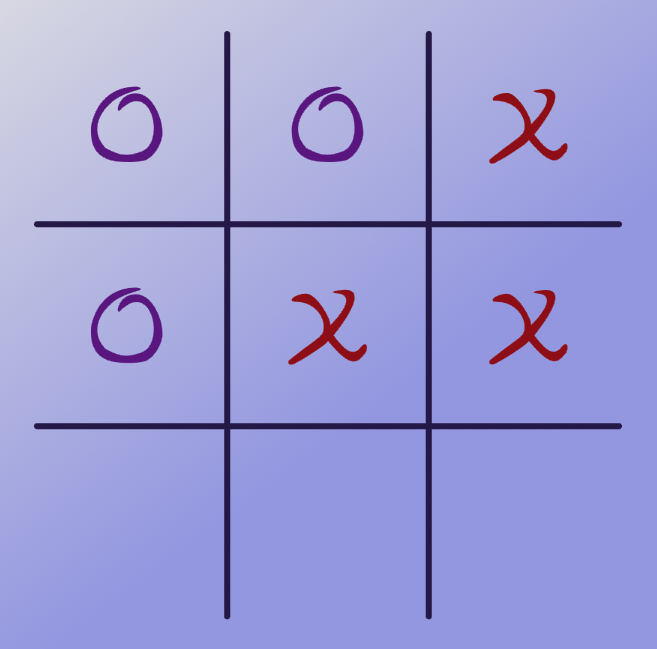
Given a sample tic tac toe board with X to move
There are three available squares for X to place a token. The first and third of these results in a score of +1 with an immediate win for X and the end of the game. The second results in the game continuing and switching to Player O's turn. There are two options available to player O, one results in three-in-a-row for O and a score of -1. Player O will always choose the minimum option so this rolls up to the layer above to be -1. So the next move for X is a choice between +1 and -1 and +1 will be chosen. When there are two options of equal value, the first choice can be taken.
This process explains why Minimax is a type of Backtracking algorithm. Each possible move is taken to determine if this is a winning move and then backtracked and non-winning moves abandoned.
This same process can be followed from the beginning of a tic tac toe game, but as there are 9 initial options, each with 8 second options, plotting a diagram for this would be challenging.
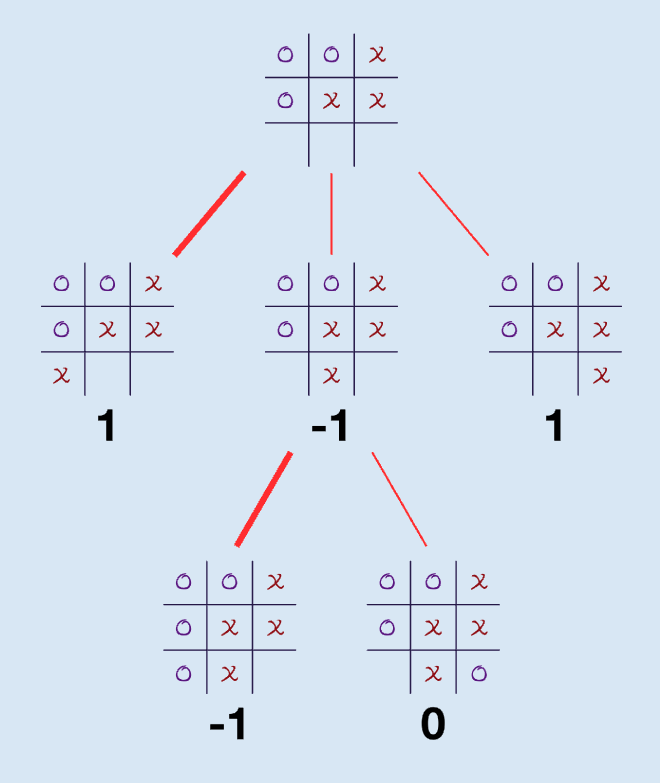
Options for X player in tic tac toe game
Pseudocode for Minimax algorithm
I will implement the minimax algorithm in Swift in the next article to allow a player to play tic tac toe against the computer. Here is pseudocode for the algorithm. There can be variations on this for more complicated games where a depth can be set to limit the number of recursions, but for tic tac toe, this is not required.
1function minimax_recursive(node, isMaximising)
2{
3 If game is over
4 return board score
5 If isMaximising
6 bestValue = negInfinity
7 For each valid move on the board
8 value = minimax_recursive(node, false)
9 bestValue = max(value, bestValue)
10 return bestValue
11 Else // Minimising
12 bestValue = posInfinity
13 For each valid move on the board
14 value = minimax_recursive(node, true)
15 bestValue = min(value, bestValue)
16 return bestValue
17}
Conclusion
The Minimax algorithm can be used to play two player games such as checkers, chess and tic tac toe. This article has come up in the middle of writing a tic tac toe app using Test Driven Development. The next article will use this minimax algorithm to allow a player to play the computer.