Fibonacci sequence and recursion
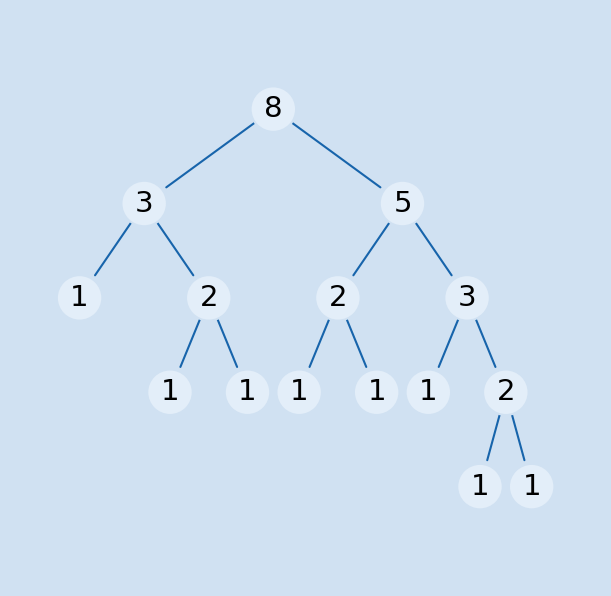
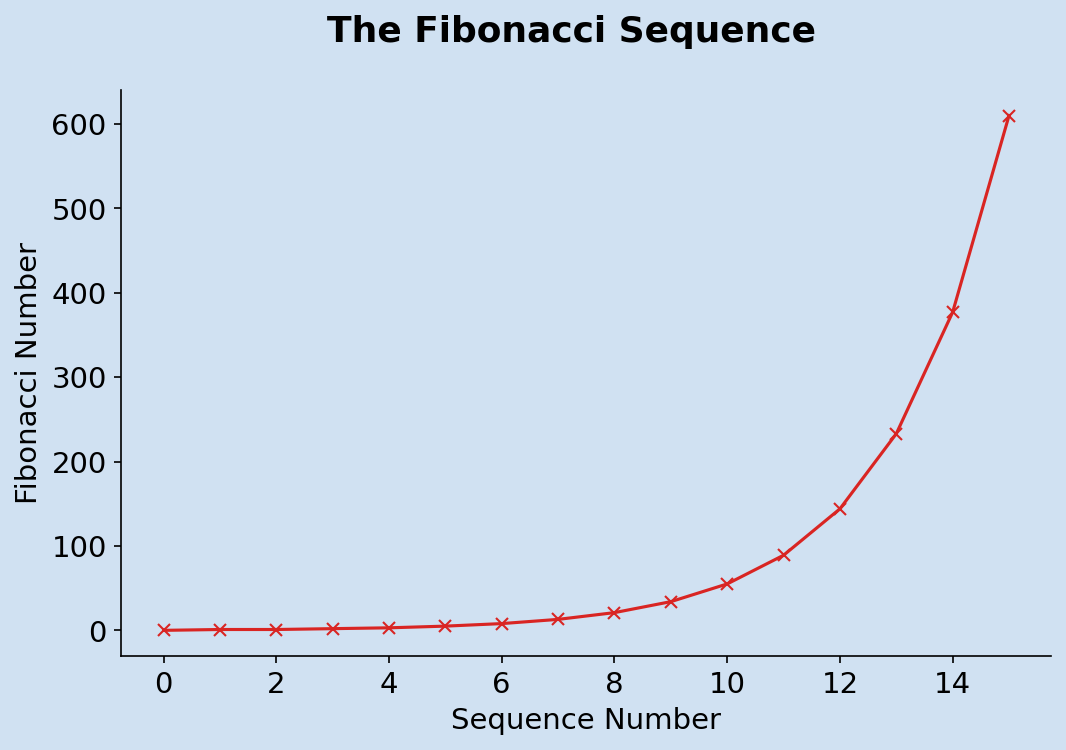
The Fibonacci sequence is a series of numbers where each number in the sequence is the sum of the preceding two numbers, starting with 0 and 1. It is natural to consider a recursive function to calculate a subset of the Fibonacci sequence, but this may not be the most efficient mechanism.
The fibonacci sequence is one of the most famous mathematical sequences. Fibonacci numbers are named after Italian mathematician Leonardo Pisano Bogollo, also known as Fibonacci. Fibonacci introduced the sequence to Western European mathematics, although the sequence was known earlier in Indian mathematics.
The first numbers in the Fibonacci sequence
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sum | -- | -- | 0 + 1 | 1 + 1 | 1 + 2 | 2 + 3 | 3 + 5 | 5 + 8 | 8 + 13 | 13 + 21 | 21 + 34 |
| Fibonacci | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Recursion
Recursion occurs when something is defined in terms of itself. It is said that recursion is one of the most natural things, yet it can be tricky to wrap your head around. In programming it is a function tha calls itself. When creating a recursive function, the first thing to consider is the exit path, in that how will the recursion end.
Recursion can be used to solve many problems with few lines of code and great code reuse. However, it may not always be the best algorithm for a task.
Fibonacci sequence using recursive function
The following function calculates the nth term in the Fibonacci sequence. This is just a few lines of code and works well for smaller numbers, but the function takes longer and longer as the numbers grows. The reason for this is that there is double recursion in each call and lots of repetition during calls.
1func fibRecursion(_ n: Int) -> Int {
2 if n < 2 {
3 return n
4 } else {
5 return fibRecursion(n-1) + fibRecursion(n-2)
6 }
7}
8
9print("fib(2) = \(fibRecursion(2))")
10print("fib(6) = \(fibRecursion(6))")
11print("fib(15) = \(fibRecursion(15))")
12
13"""
14fib(2) = 1
15fib(6) = 8
16fib(15) = 610
17"""
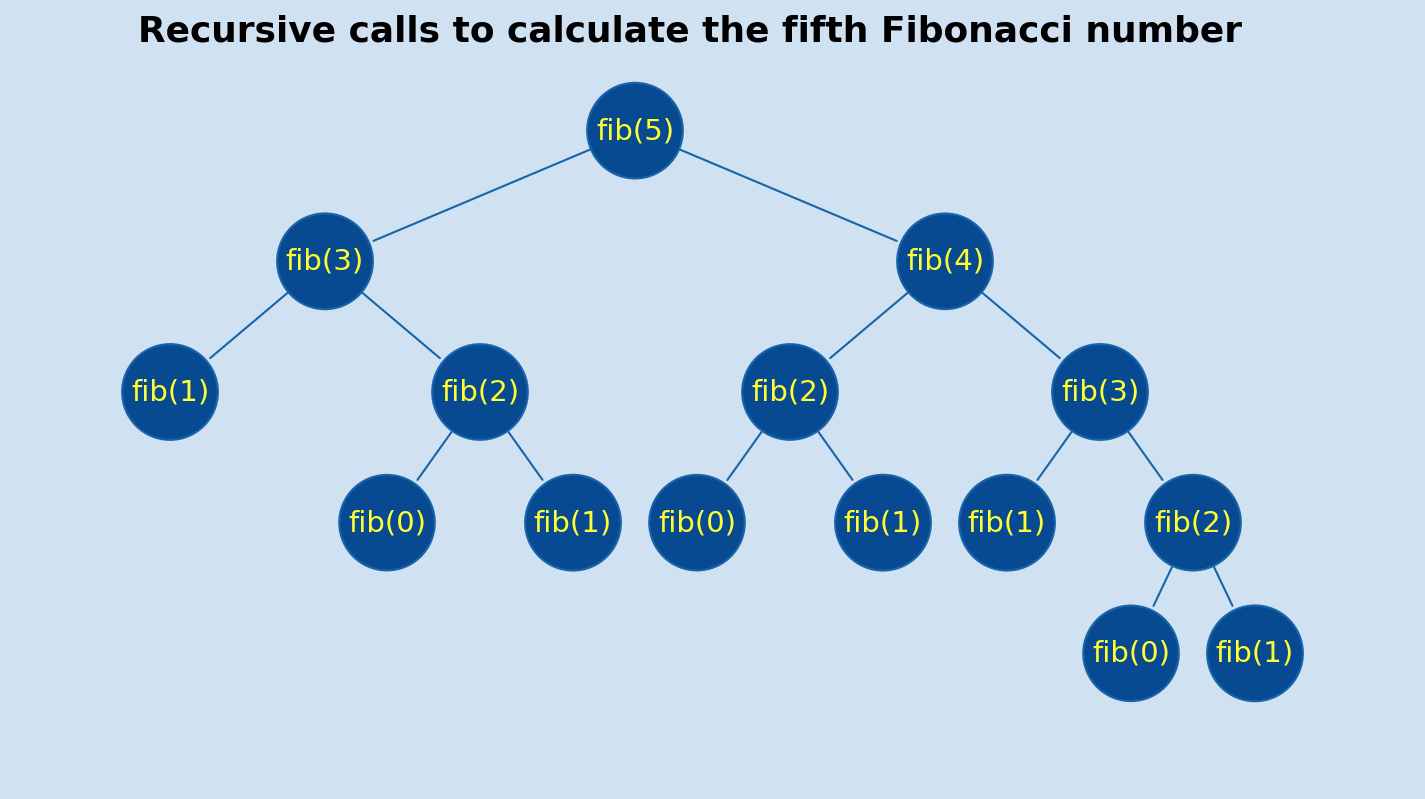
Excessive calls
A closer look at this function shows that it is incredibly inefficient. The diagram shows how the function is called to calculate the fifth fibonacci number. Each call to this function calls itself two times and because it is recursive, this doubling is increased exponentially as the number grows. The function is called 15 times to calculate the fifth fibonacci number, this may not seem too bad, but it is called 21,891 times to calculate the 20th Fibonacci number.
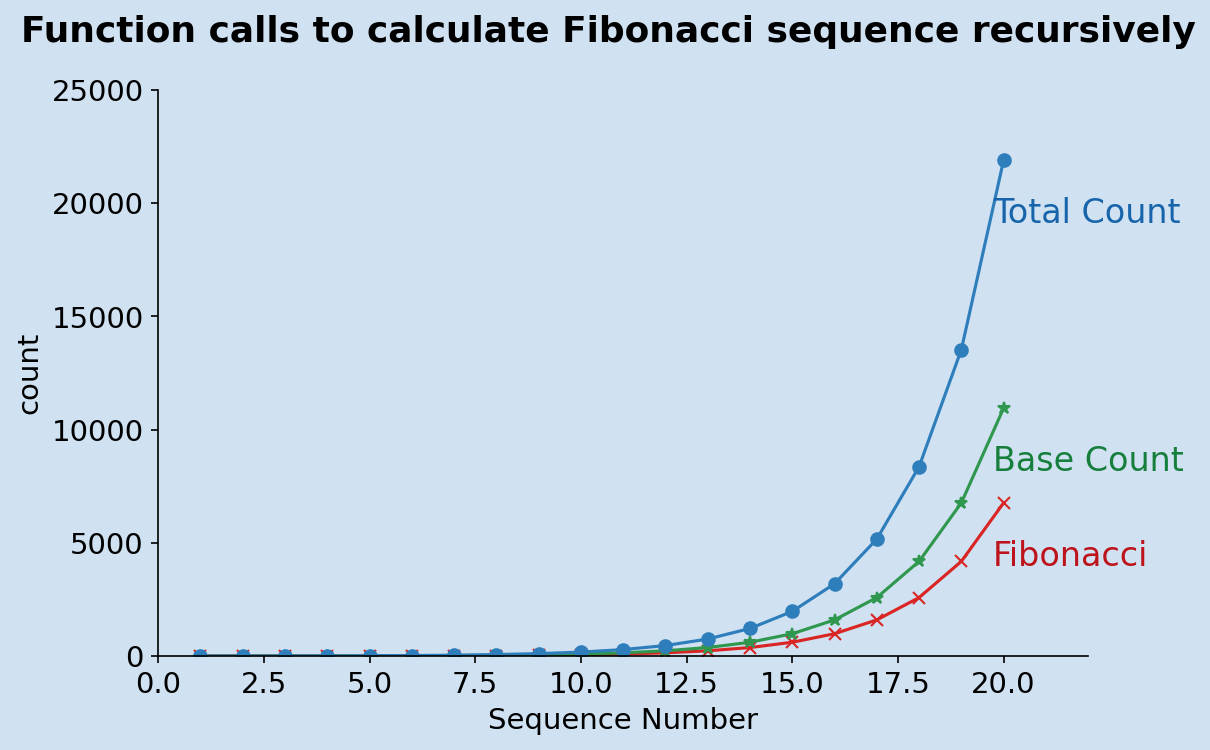
The recursive function is modified to collect how many times the function is called when calculating a number of Fibonacci numbers. Counters are used to count how many times the function is called and how many times the base case of the recursion is called.
The table shows the number of function calls for the first 20 Fibonacci numbers.
1var baseCount = 0
2var totalCount = 0
3func fibRecursionCount(_ n: Int) -> Int {
4 totalCount += 1
5 if n < 2 {
6 baseCount += 1
7 return n
8 } else {
9 return fibRecursionCount(n-1) + fibRecursionCount(n-2)
10 }
11}
1var results = [[Int]]()
2for i in 1...20 {
3 baseCount = 0
4 totalCount = 0
5 let fib = fibRecursionCount(i)
6 results.append([i, fib, baseCount, totalCount])
7}
Number of recursive function calls to get Fibonacci numbers
| Index | Fibonacci | Base Count | Total Count |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 3 |
| 3 | 2 | 3 | 5 |
| 4 | 3 | 5 | 9 |
| 5 | 5 | 8 | 15 |
| 6 | 8 | 13 | 25 |
| 7 | 13 | 21 | 41 |
| 8 | 21 | 34 | 67 |
| 9 | 34 | 55 | 109 |
| 10 | 55 | 89 | 177 |
| 11 | 89 | 144 | 287 |
| 12 | 144 | 233 | 465 |
| 13 | 233 | 377 | 753 |
| 14 | 377 | 610 | 1,219 |
| 15 | 610 | 987 | 1,973 |
| 16 | 987 | 1,597 | 3,193 |
| 17 | 1,597 | 2,584 | 5,167 |
| 18 | 2,584 | 4,181 | 8,361 |
| 19 | 4,181 | 6,765 | 13,529 |
| 20 | 6,765 | 10,946 | 21,891 |
Memoization
The chart above shows that there are a lot of repeat calls to the function with the same parameter, yielding the same result. Memoization is an optimisation technique, where the results of functions are cached and returned instead of computing the same operation again. Memoization is used in this variation of the recursive function to return a cached value for a function call or to store the value when it is not in the cache. The recursive function is defined inside a regular function as well as the cache, which is a dictionary.
1func fibMemoization(_ n: Int) -> Int {
2 var fibMemo: [Int: Int] = [0: 0, 1: 1]
3 func fibMemRec(_ n: Int) -> Int {
4 if let result = fibMemo[n] {
5 return result
6 } else {
7 fibMemo[n] = fibMemRec(n - 1) + fibMemRec(n - 2)
8 }
9 return fibMemo[n]!
10 }
11 return fibMemRec(n)
12}
For loop
The Fibonacci sequence of numbers could also be calculated in a more straight forward way using a loop.
1func fibLoop(_ n: Int) -> Int {
2 if (n == 0) {
3 return n
4 }
5 var (last, next) = (0, 1)
6 for _ in 1..<n {
7 (last, next) = (next, last + next)
8 }
9 return next
10}
Golden Ratio
There is another way to calculate the Fibonacci sequence of numbers using the Golden Ratio.
The Golden ratio is a constant 1.6180339887 represented by the Greek letter phi φ
$$ \varphi ={\frac {1+{\sqrt {5}}}{2}}=1.6180339887 $$
This feels like a bit of a cheat, but it is based on the fact that the ratio of two successive Fibonacci numbers is close to the Golden ratio and is more accurate as the numbers increase. Therefore the next Fibonacci number is calculated by multiplying the current number by the ratio and rounding the number to the nearest Integer. This brings us back to using a recursive function that takes two parameters; the depth of recursion, based on the sequence number; and the current Fibonacci number, starting at 1. This recursive function is internal to a function that just takes one number.
1func fibGolden(_ num: Int) -> Int{
2 let goldenRatio = (1.0 + pow(5.0, 0.5)) / 2.0
3 func fibGoldenRec(_ depth: Int, _ n: Int) -> Int{
4 if depth <= 2 {
5 return n
6 }
7 return fibGoldenRec(depth-1, Int(round(Double(n) * goldenRatio)))
8 }
9 return fibGoldenRec(num, 1)
10}
Comparison of the four methods
The 4 methods to calculate the first 20 Fibonacci numbers were timed to see which one performed the best. The time to execute the different functions was measured using Date from Foundation, using the average of 20 repeat calls.
1func TimeFunction(repeats:Int, function: (Int)->Int, num:Int) -> (Double,[Double]) {
2 var results:[Double] = []
3 var averageTime = 0.0
4 for _ in 1...repeats {
5 let startTime = Date()
6 function(num)
7 let endTime = Date()
8 let timetaken = DateInterval(start: startTime, end: endTime)
9 results.append(timetaken.duration * 1000.0)
10 }
11 averageTime = results.reduce(0,+) / Double(results.count)
12 return (averageTime, results)
13}
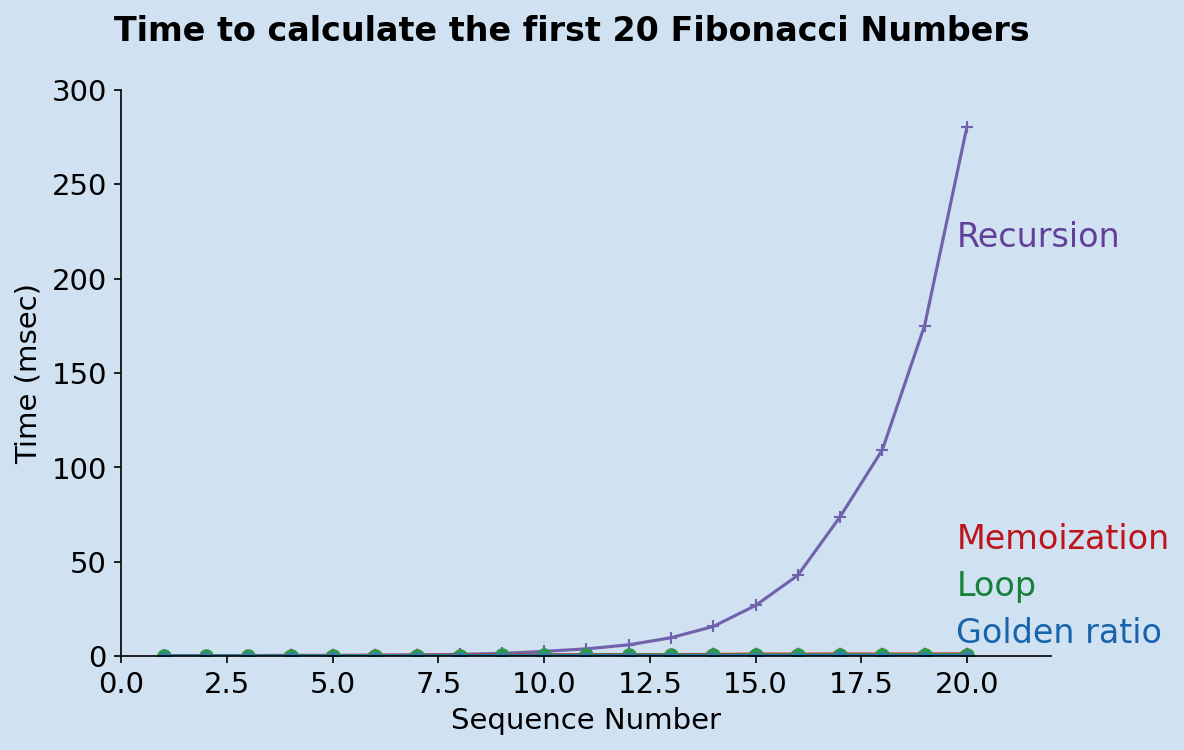
The initial recursive method performs terribly as predicted. Excluding this method the other functions were timed for the first 50 Fibonacci numbers. This shows that use of Memoization is significantly better than the initial recursive function. However, the for loop is probably easiest to understand and outperforms either of the two recursive functions. The best performance is achieved using recursion with the Golden ratio and this requires knowledge of the nature and properties of Fibonacci numbers.
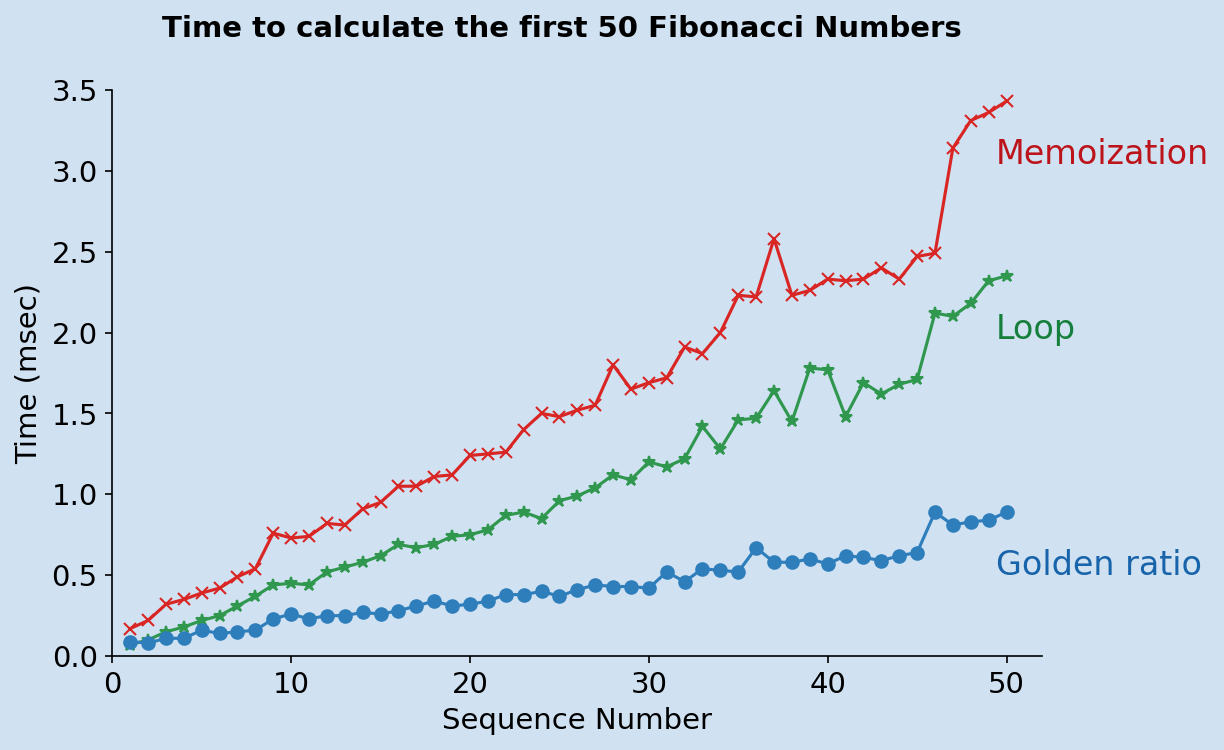
Conclusion
Recursion may seem like a natural approach for calculating the sequence of the Fibonacci numbers. It can be written easily, but each call to the function results in two more calls to the function and there is excessive repetition involved resulting in this approach being unsuitable. Memoization is the caching of function results and can be used to significantly reduce the repetition, but it can make the code harder to read and maintain. A straight forward loop is a better approach to calculating the Fibonacci numbers as it is easier to understand and maintain and it performs better. A recursive function can be used with a calculation using the Golden ratio and this does not have the compounding calls or performance hits as the initial recursive function. In fact, use of the Golden ratio out performed all other methods in this experiment.