Water pouring puzzle
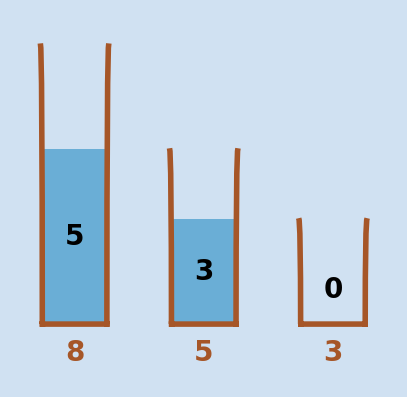
We came across the water pouring puzzle again recently and there was some discussion on where to start and explain how to slove it. The specific puzzle we came across was given two containers of sizes 7 and 4 litres, measure out a volume of water that is exactly 5 litres. A tap is available to refill the containers and a sink or drain in which to discard water.
There are a number of variations of this puzzle, including a famous example of this in a scene of the 1995 movie Die Hard with a Vengeance. In the example in the movie the containers are 5 and 3 gallons and the challenge is to fill the 5-gallon container with exactly 4 gallons of water.
The following rules usually apply
- The containers in the puzzle are irregularly shaped and unmarked, so that it is impossible to accurately measure any quantity of water that does not completely fill a container.
- Each step pouring water from a source container to a destination container stops when either the source container is empty or the destination container is full, whichever happens first.
How many containers
There are versions of the water pouring puzzle that have three containers. One example is a containers of 8, 5 and 3. Starting with the 8 container full, how to get to a state of exactly 4 units in each of the 8 and 5 containers. The 8, 5 & 3 containers is the same as the 5 & 3 container with the 8 container acting as both the sink and the drain.
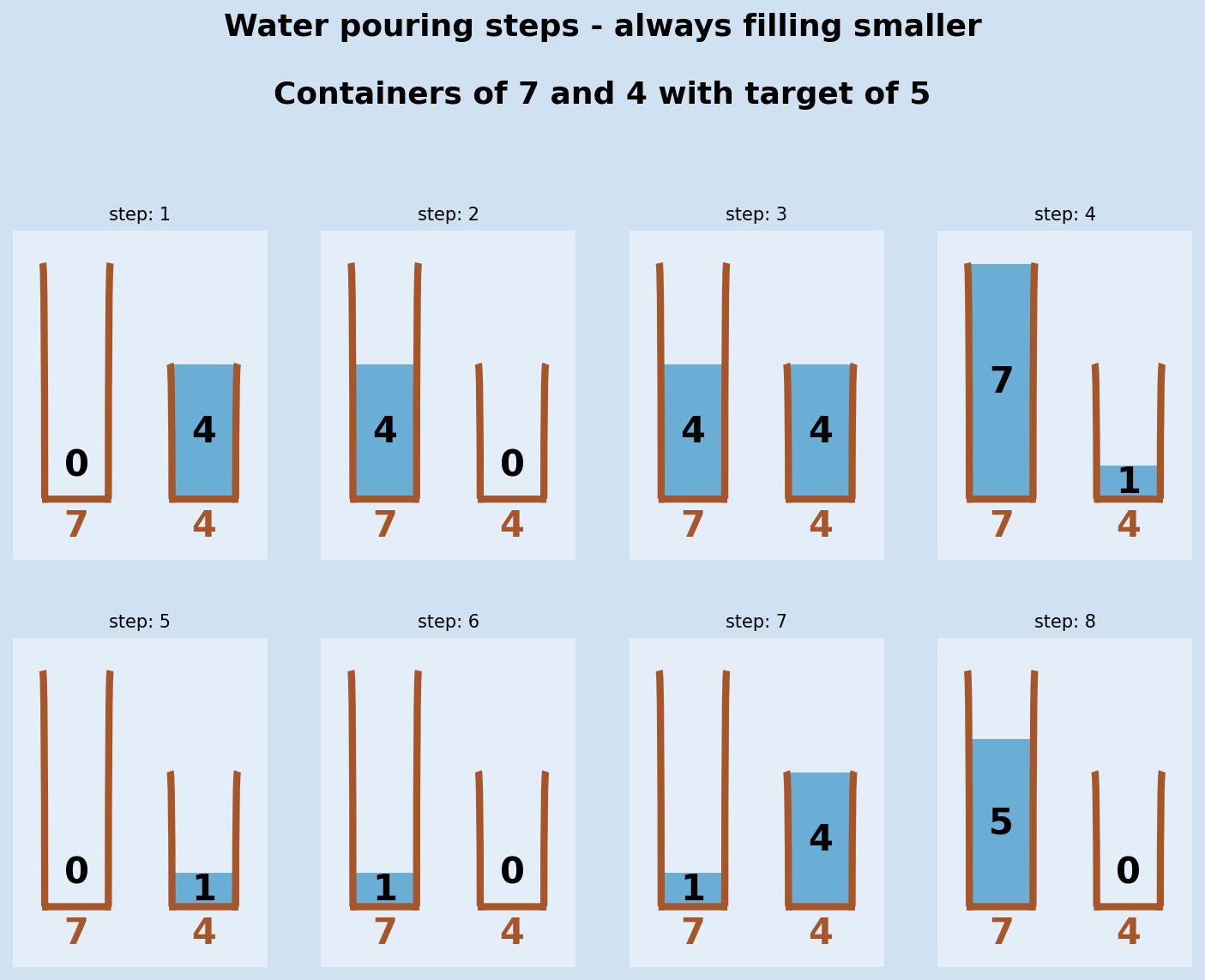
How to solve the problem with containers 7,4 and target 5
I have come across this puzzle before, and solved it by picturing containers in my head and pouring water back and forth. Alternatively, one can scribble on a piece of paper the different volumes of water in each container as they change. Eventually a solution can be found where the volumes in the containers changes as outlined in the following table.
Steps to get a volume of 5 from two containers of 7 and 4
| Step | Larger (7) | Smaller (4) |
|---|---|---|
| 0 | 0 | 4 |
| 1 | 4 | 0 |
| 2 | 4 | 4 |
| 3 | 7 | 1 |
| 4 | 0 | 1 |
| 5 | 1 | 0 |
| 6 | 1 | 4 |
| 7 | 5 | 0 |
Can a program be written to solve this puzzle? The short answer is yes, but one needs to figure out what the logic is to solving it. A closer look at the solution above shows that the key is to always fill the smaller container from the tap, empty it into the larger container and only empty the larger container into the sink. Here is a graphical representation of this solution.
It turns out that this is not the only solution to this puzzle. The desired volume can also be reached by always filling the larger container from the tap and only emptying the smaller container into the sink.
So the real algorithm to solving this problem is to pick one container and always fill that one from the tap, empty the first container into the second and only empty the second into the sink.
Steps to solve
- Fill first container from tap when empty
- Top up second container with water from first container
- Empty second container into sink when full
- Repeat steps 1 to 3 until the desired volume is reached
Container class
A Container class is created to represent the container. It has two properties for
the container capacity and how much is available. It also has methods to add,
remove, fill and empty.
1class Container:
2 def __init__(self, capacity):
3 self.capacity = capacity
4 self.available = capacity
5
6 def __repr__(self):
7 return f"<Container - {self.capacity}, {self.available}>"
8
9 def __str__(self):
10 return f"Size {self.capacity} Container with {self.available} available"
11
12 @property
13 def content(self):
14 return self.capacity - self.available
15
16 def add(self, vol):
17 added = vol
18 if vol > self.available:
19 added = self.available
20 self.available = 0
21 else:
22 self.available = self.available - vol
23 return added
24
25 def remove(self, vol):
26 if vol > self.content:
27 self.available = self.capacity
28 else:
29 self.available = self.available + vol
30
31 def fill(self):
32 self.available = 0
33 self.current = self.capacity
34
35 def empty(self):
36 self.available = self.capacity
37 self.current = 0
The following code is used to exercise the class to ensure it is working correctly.
1c7 = Container(7)
2print(f"New container: {c7}")
3
4c7.fill()
5print(f"After fill: {c7}")
6
7c7.remove(4)
8print(f"After remove 4: {c7}")
9print(f"c7 content = {c7.content}")
10
11c7.empty()
12print(f"After empty: {c7}")
13
14c7.add(12)
15print(f"After add 12: {c7}")
16print(f"c7 content = {c7.content}")
17
18"""
19output:
20
21New container: Size 7 Container with 7 available
22After fill: Size 7 Container with 0 available
23After remove 4: Size 7 Container with 4 available
24c7 content = 3
25After empty: Size 7 Container with 7 available
26After add 12: Size 7 Container with 0 available
27c7 content = 7
28"""
Always fill the smaller container
The first approach to solving the water pouring puzzle is to always fill the smaller container from a tap. Using the class above for the containers, the following function determines the number of steps to reach a state where a container has the desired target volume. This function returns a list of dictionaries that contain the current content for each of the containers.
This program could be improved by adding more error checking, such as ensuring that the containers are not the same size or ensuring the target is not greater than the larger container size.
1def smaller_to_larger(large, small, target, max_steps=20):
2 steps = []
3 larger = Container(large)
4 smaller = Container(small)
5 for i in range(1, max_steps):
6 if larger.available == 0: # Empty larger container if it is full
7 larger.empty()
8 elif smaller.content == 0: # Fill the smaller container if it is empty
9 smaller.fill()
10 else:
11 smaller.remove(larger.add(smaller.content))
12 step = {large: larger.content, small: smaller.content}
13 steps.append(step)
14
15 if larger.content == target or smaller.content == target:
16 print(
17 f"Target '{target}' met after {i} steps: Large = {larger.content}, Small = {smaller.content}"
18 )
19 break
20 else:
21 print(f"Target '{target}' not reached after {i} steps")
22 return steps
23
24
25steps = smaller_to_larger(7, 4, 5)
26
27"""
28[{7: 0, 4: 4},
29 {7: 4, 4: 0},
30 {7: 4, 4: 4},
31 {7: 7, 4: 1},
32 {7: 0, 4: 1},
33 {7: 1, 4: 0},
34 {7: 1, 4: 4},
35 {7: 5, 4: 0}]
36"""

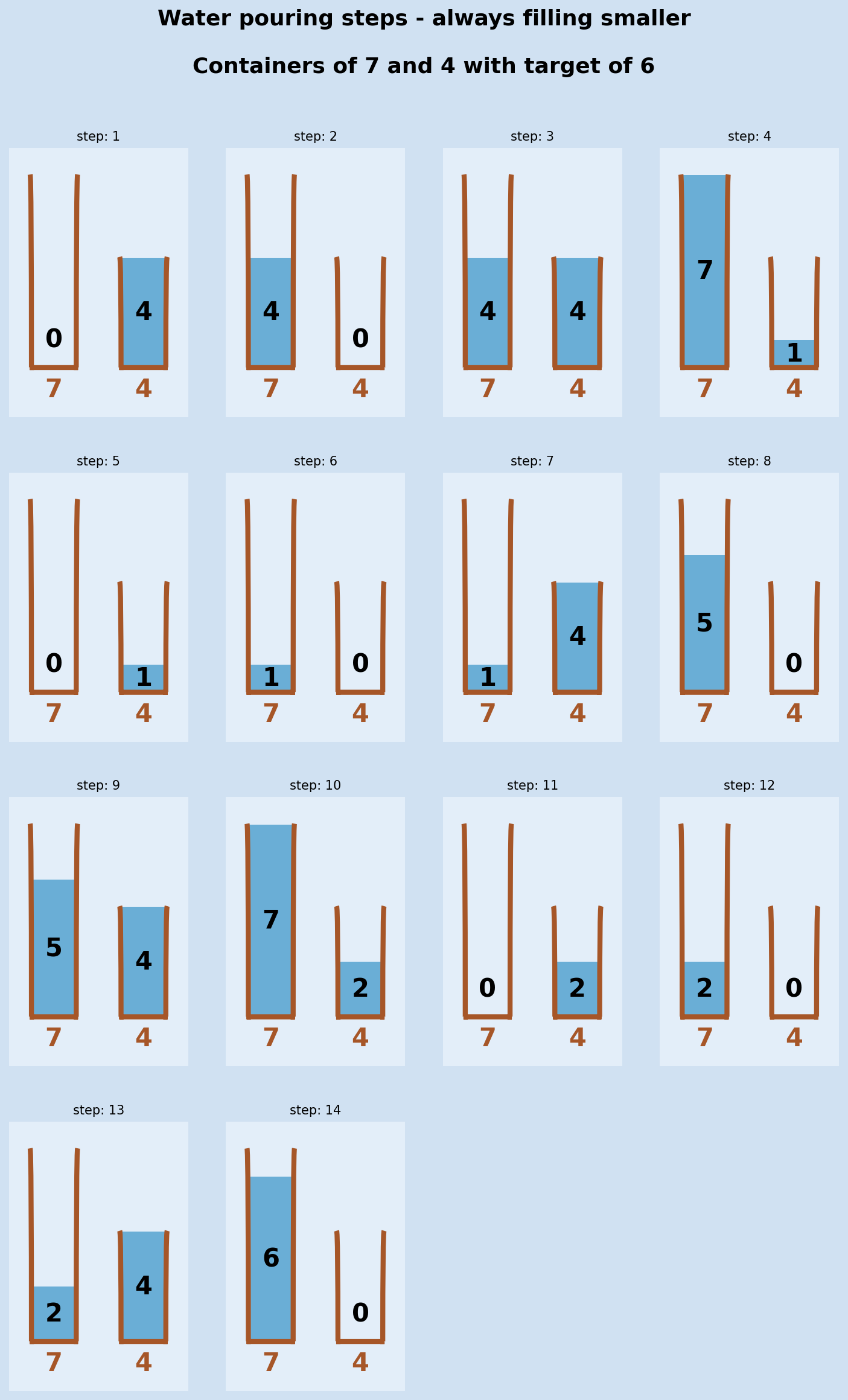
The same function can be called for the same containers, but with a target size of 6 or with different containers and target size.
1steps = smaller_to_larger(7, 4, 6)
2
3steps
4"""
5[{7: 0, 4: 4},
6 {7: 4, 4: 0},
7 {7: 4, 4: 4},
8 {7: 7, 4: 1},
9 {7: 0, 4: 1},
10 {7: 1, 4: 0},
11 {7: 1, 4: 4},
12 {7: 5, 4: 0},
13 {7: 5, 4: 4},
14 {7: 7, 4: 2},
15 {7: 0, 4: 2},
16 {7: 2, 4: 0},
17 {7: 2, 4: 4},
18 {7: 6, 4: 0}]
19"""
Containers of sizes 5 and 3 with target volume of 4.
1steps = smaller_to_larger(5, 3, 4)
2
3steps
4"""
5[{5: 0, 3: 3},
6 {5: 3, 3: 0},
7 {5: 3, 3: 3},
8 {5: 5, 3: 1},
9 {5: 0, 3: 1},
10 {5: 1, 3: 0},
11 {5: 1, 3: 3},
12 {5: 4, 3: 0}]
13"""
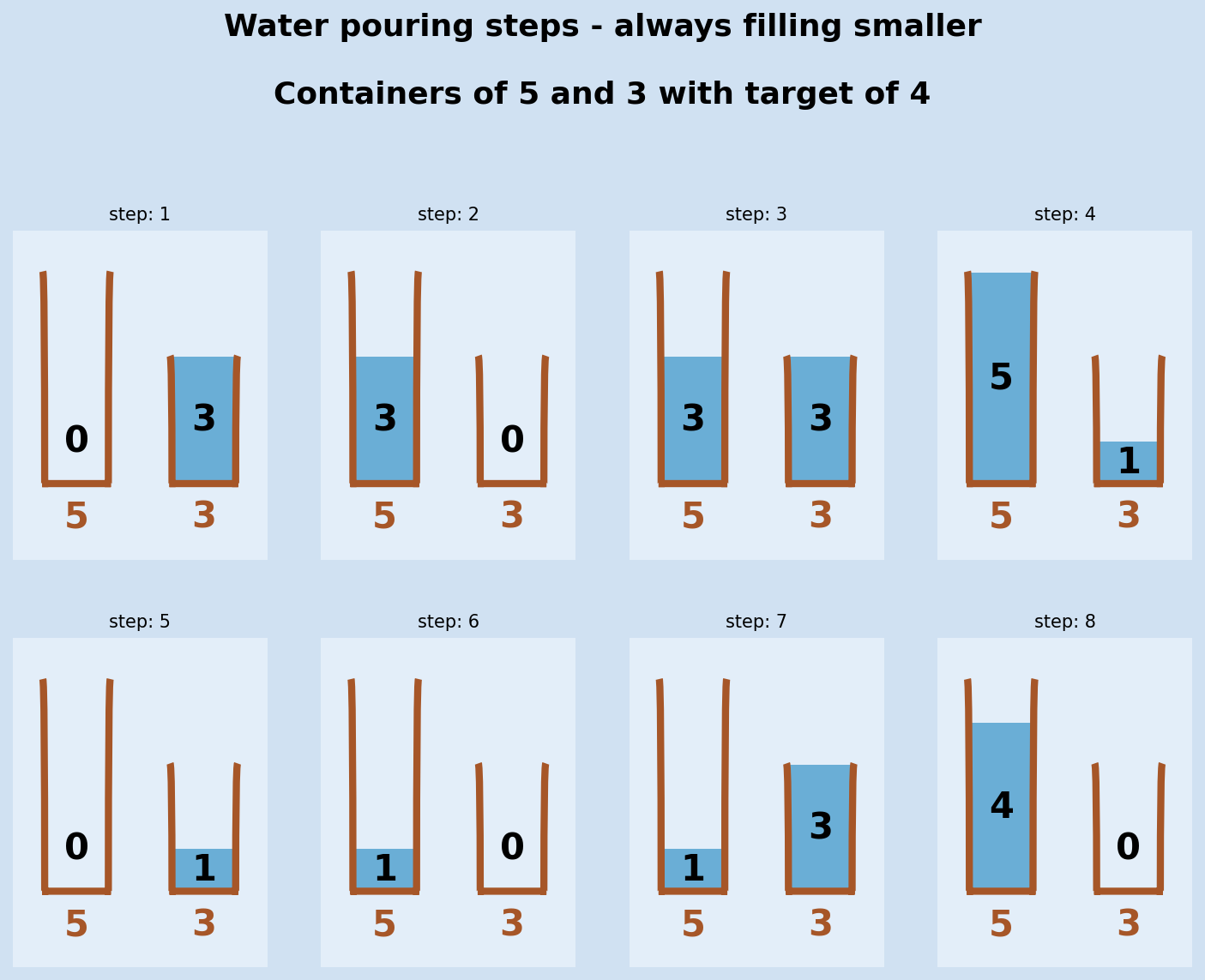
Always fill the larger container
This is a similar approach to the previous except that the larger container is always filled from the tap, the larger tops up the smaller container and only the smaller container is emptied into the sink.
1def larger_to_smaller(large, small, target, max_steps=20):
2 steps = []
3 larger = Container(large)
4 smaller = Container(small)
5 for i in range(1, max_steps):
6 if smaller.available == 0: # Empty smaller container if it is full
7 smaller.empty()
8 elif larger.content == 0: # Fill the larger container if it is empty
9 larger.fill()
10 else:
11 larger.remove(smaller.add(larger.content))
12 step = {large: larger.content, small: smaller.content}
13 steps.append(step)
14
15 if larger.content == target or smaller.content == target:
16 print(
17 f"Target '{target}' met after {i} steps: Large = {larger.content}, Small = {smaller.content}"
18 )
19 break
20 else:
21 print(f"Target '{target}' not reached after {i} steps")
22 return steps
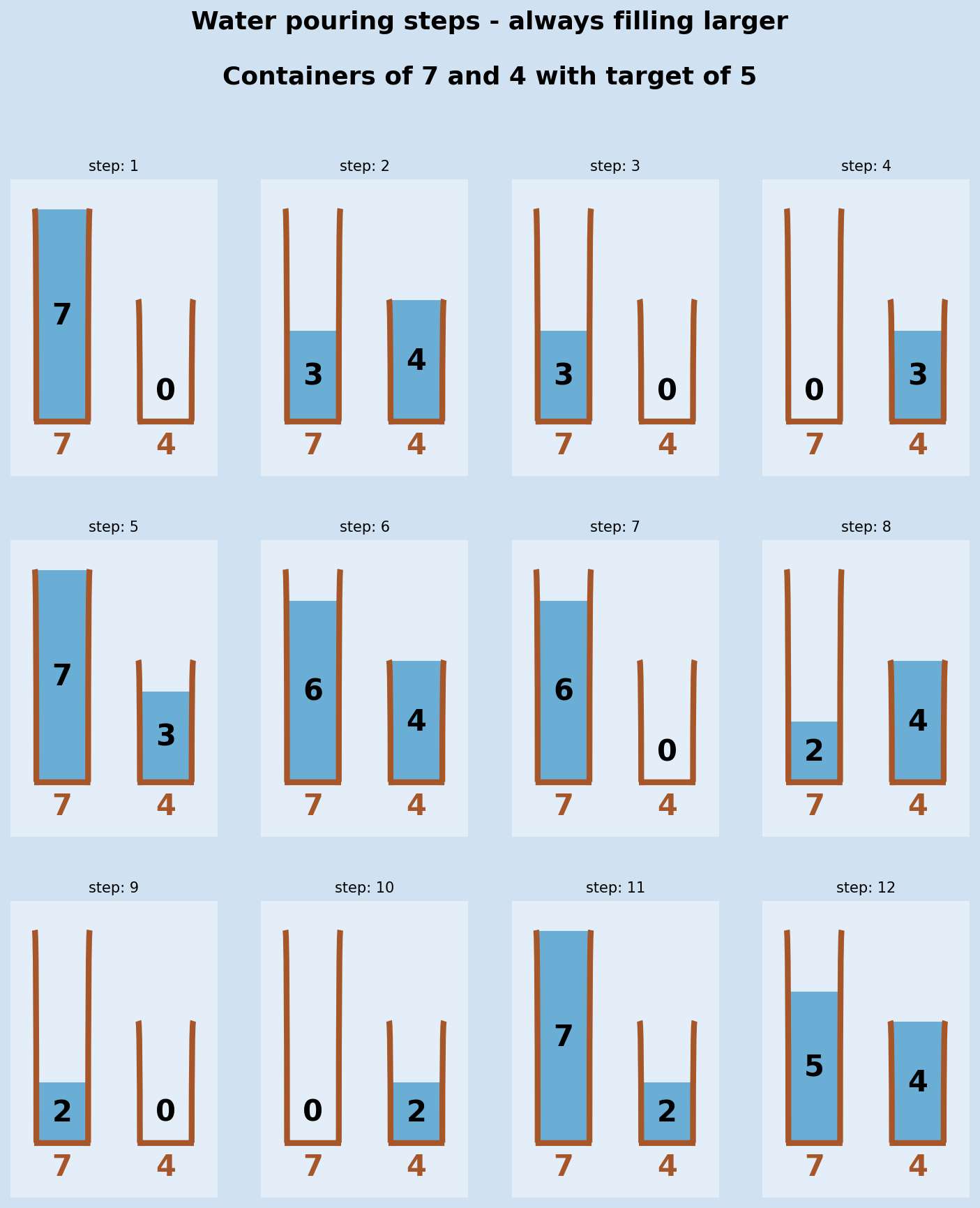
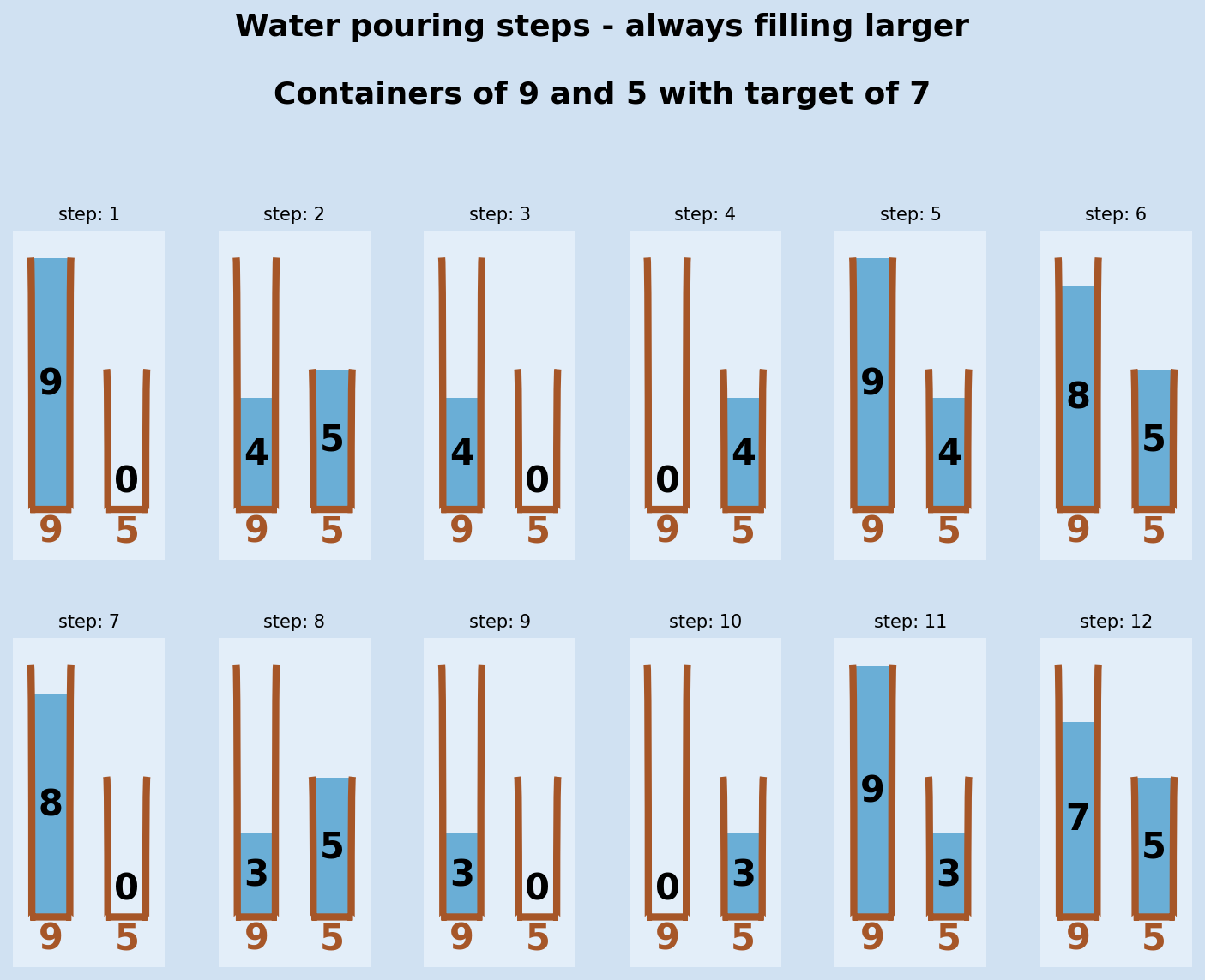
Combine the two functions
The two functions smaller_to_larger and larger_to_smaller are very similar and share
a lot of the same code. These can be combined into a single function with a flag
parameter as to whether to start with the smaller or larger container.
Note that in these functions a for loop is used with a maximum number of steps to interate through the loop. Intuitively, this could be changed to a while loop that would continue while the target is NOT met. However, there is a risk of setting the containers and a target that could not be reached and then this function would enter an infinite loop. Consider a larger container of 8 and a smaller container of 4, then a target of 5 could not be reached.
The other change in this function is to return a tuple of the steps list and a boolean value as to whether the target was met or not.
1def steps_to_target(large, small, target, large_first=False, max_steps=20):
2 steps = []
3 target_met = False
4 first, second = Container(small), Container(large)
5 if large_first:
6 first, second = Container(large), Container(small)
7
8 for i in range(1, max_steps):
9 if second.available == 0: # Empty second container if it is full
10 second.empty()
11 elif first.content == 0: # Fill the first container if it is empty
12 first.fill()
13 else:
14 first.remove(second.add(first.content))
15
16 step = {second.capacity: second.content, first.capacity: first.content}
17 if large_first:
18 step = {first.capacity: first.content, second.capacity: second.content}
19 steps.append(step)
20
21 if first.content == target or second.content == target:
22 target_met = True
23 break
24 else:
25 steps = []
26
27 return steps, target_met
1steps, success = steps_to_target(9, 5, 7)
2
3success
4"""
5True
6"""
7
8steps
9"""
10[{9: 0, 5: 5},
11 {9: 5, 5: 0},
12 {9: 5, 5: 5},
13 {9: 9, 5: 1},
14 {9: 0, 5: 1},
15 {9: 1, 5: 0},
16 {9: 1, 5: 5},
17 {9: 6, 5: 0},
18 {9: 6, 5: 5},
19 {9: 9, 5: 2},
20 {9: 0, 5: 2},
21 {9: 2, 5: 0},
22 {9: 2, 5: 5},
23 {9: 7, 5: 0}]
24"""
25
26
27steps, success = steps_to_target(9, 5, 7, large_first=True)
28
29success
30"""
31True
32"""
33
34steps
35"""
36[{9: 9, 5: 0},
37 {9: 4, 5: 5},
38 {9: 4, 5: 0},
39 {9: 0, 5: 4},
40 {9: 9, 5: 4},
41 {9: 8, 5: 5},
42 {9: 8, 5: 0},
43 {9: 3, 5: 5},
44 {9: 3, 5: 0},
45 {9: 0, 5: 3},
46 {9: 9, 5: 3},
47 {9: 7, 5: 5}]
48"""

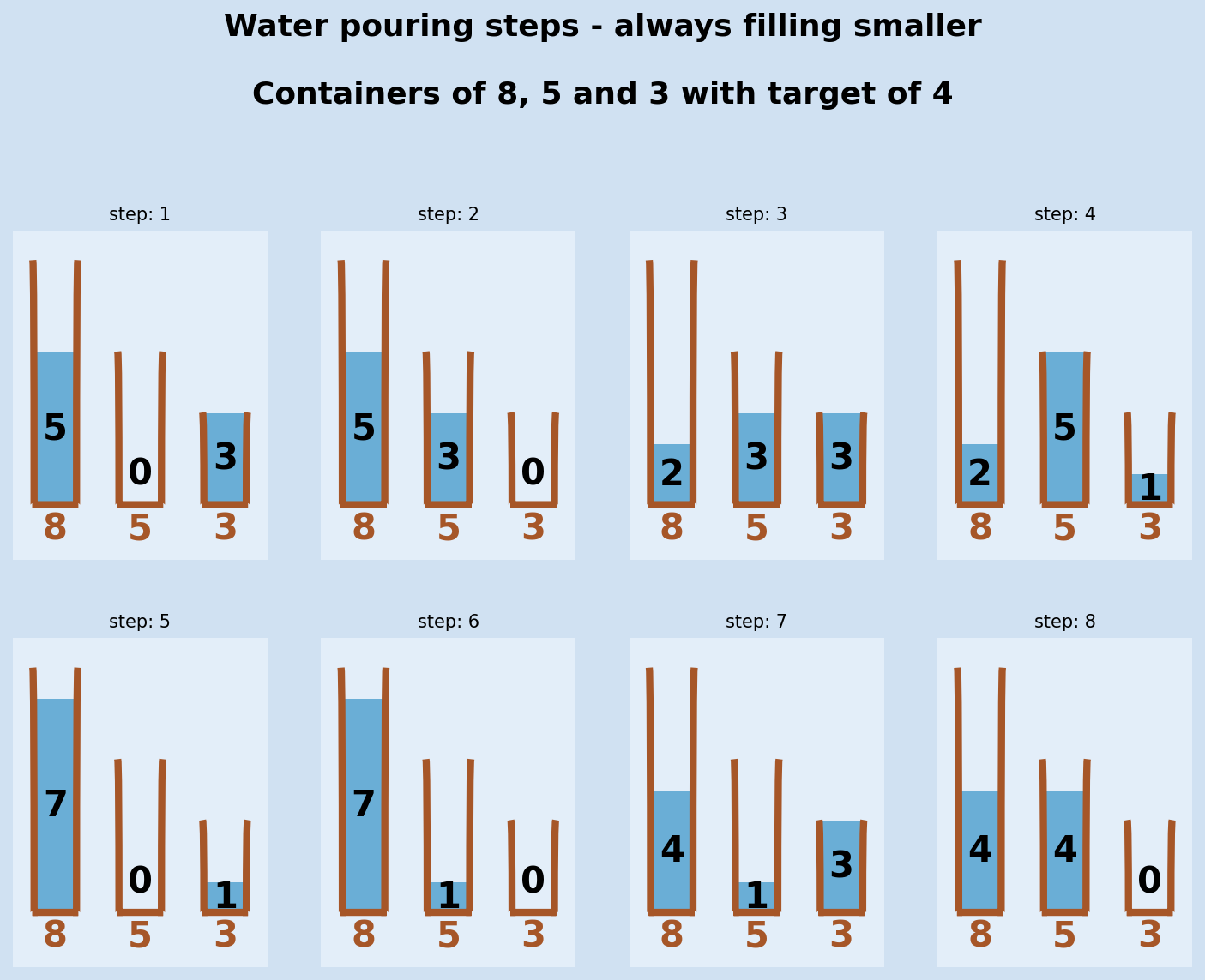
Three container version
The three container version is similar to the two container one, where the largest
container acts as both the tap and the sink. In this puzzle, no water can be added
and no water discarded and the sum of the smaller two containers is equal to the
largest container. The steps_to_target_three_containers function is based on the
previous function taking in the three container sizes. The logic in each step is
similar except that when the first container is filled, the contents of the largest
container must be reduced and when the second container is emptied, the contents of
the largest container must be increased.
1def steps_to_target_three_containers(
2 largest, medium, small, target, large_first=False, max_steps=20
3):
4 steps = []
5 target_met = False
6 tap_sink = Container(largest)
7 tap_sink.fill()
8 first, second = Container(small), Container(medium)
9 if large_first:
10 first, second = Container(medium), Container(small)
11
12 for i in range(1, max_steps):
13 if second.available == 0: # Empty second container if it is full
14 second.empty()
15 tap_sink.add(second.capacity)
16 elif first.content == 0: # Fill the first container if it is empty
17 first.fill()
18 tap_sink.remove(first.capacity)
19 else:
20 first.remove(second.add(first.content))
21
22 step = {
23 tap_sink.capacity: tap_sink.content,
24 second.capacity: second.content,
25 first.capacity: first.content,
26 }
27 if large_first:
28 step = {
29 tap_sink.capacity: tap_sink.content,
30 first.capacity: first.content,
31 second.capacity: second.content,
32 }
33 steps.append(step)
34
35 if first.content == target or second.content == target:
36 target_met = True
37 break
38 else:
39 steps = []
40
41 return steps, target_met
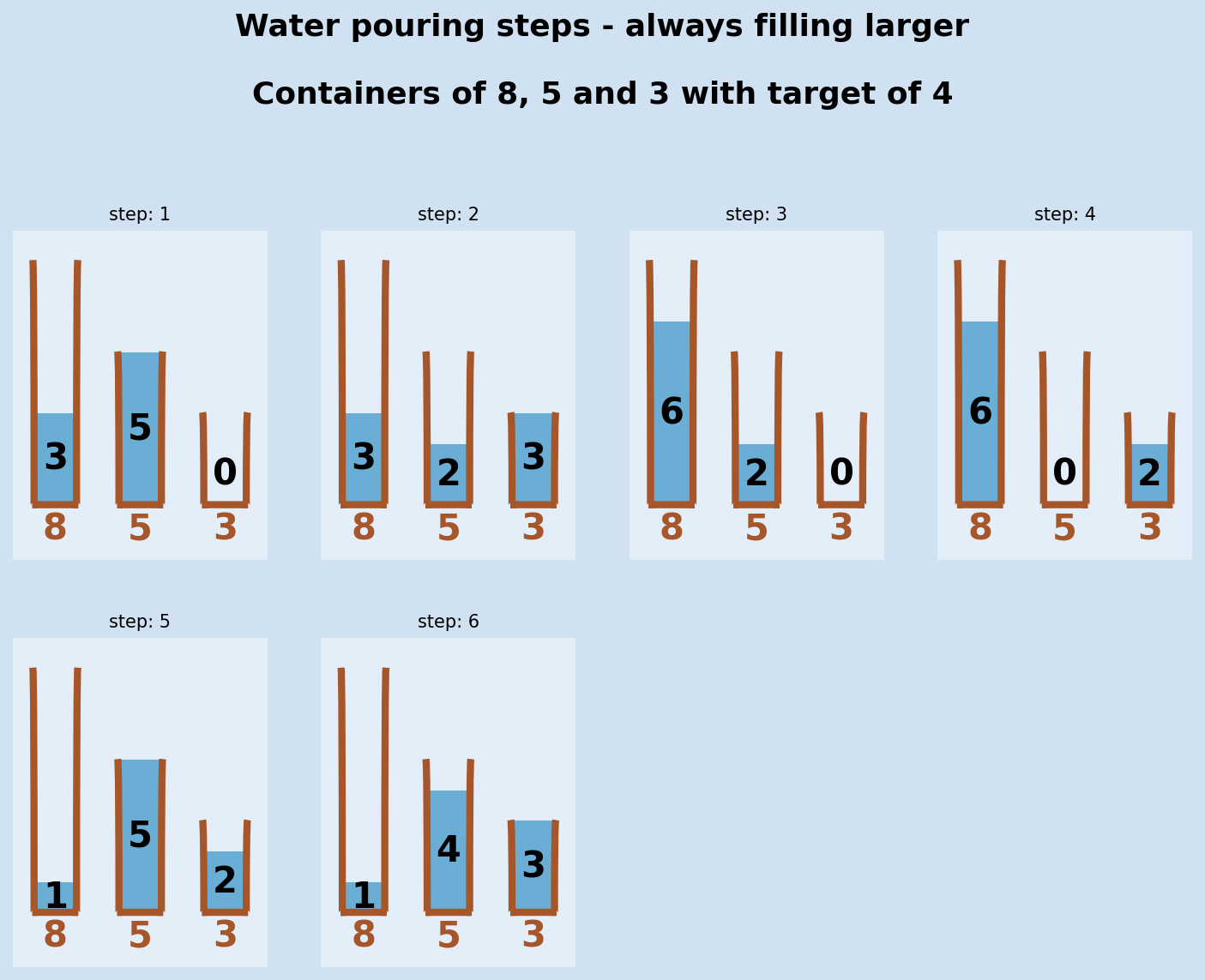
The following shows the steps to get to a target volume of 4. There are some variations of this game whereby the target is for both the 8 and 5 containers to hold 4 units each. In this case, the larger-first approach needs one more step to discard the 3 units back into the 8 container.
1steps, success = steps_to_target(8, 5, 3, 4)
2steps
3"""
4[{8: 5, 5: 0, 3: 3},
5 {8: 5, 5: 3, 3: 0},
6 {8: 2, 5: 3, 3: 3},
7 {8: 2, 5: 5, 3: 1},
8 {8: 7, 5: 0, 3: 1},
9 {8: 7, 5: 1, 3: 0},
10 {8: 4, 5: 1, 3: 3},
11 {8: 4, 5: 4, 3: 0}]
12"""
13
14
15steps, success = steps_to_target(8, 5, 3, 4, large_first=True)
16steps
17"""
18[{8: 3, 5: 5, 3: 0},
19 {8: 3, 5: 2, 3: 3},
20 {8: 6, 5: 2, 3: 0},
21 {8: 6, 5: 0, 3: 2},
22 {8: 1, 5: 5, 3: 2},
23 {8: 1, 5: 4, 3: 3}]
24"""
Conclusion
I have come across the water pouring puzzle before and I managed to solve it by trial and error. I had not seen a generic solution to this, even when I had solved it. The difference this time is that one person identified the solution for 7, 4, target 5 as starting with the 4-container and another person identified the solution as starting with the 7-container. As shown in this article both approaches work, the key to any solution is to always fill the same container.