How to animate a Shape change in SwiftUI

Building on previous articles on Path animation in SwiftUI, this article demonstrates how to animate the smooth transition form one random shape to another. This is done by defining a custom AnimatableData for a list of cubic curves and using this in a custom shape so that SwiftUI can present a smooth transition from one shape to another.
This is the sixth article in a series on SwiftUI animation:
- Animating a shape change in SwiftUI
- Create a blob shape in SwiftUI
- How to animate a line move in SwiftUI
- How to animate a quadratic curve change in SwiftUI
- How to animate a Cubic Curve change in SwiftUI
- How to animate a Shape change in SwiftUI
Creating a random shape
A structure is defined for a CubicSegment that holds the end point and two control
points to create the cubic Bézier curve. The function CreateRandomShape takes in
the number of sides or segments in the shape and creates that number of random cubic
Bézier curves around a central point in a 1 by 1 frame.
1struct CubicSegment {
2 let point: CGPoint
3 let control1: CGPoint
4 let control2: CGPoint
5}
6
7func Cartesian(length:Double, angle:Double) -> CGPoint {
8 return CGPoint(x: length * cos(angle), y: length * sin(angle))
9}
10
11func CreateRandomShape(sides:Int) -> [CubicSegment] {
12 var segments:[CubicSegment] = []
13
14 let r = 0.5
15 let c = CGPoint(x: 0.5, y: 0.5)
16 let sectorAngle = 2.0 * Double.pi / Double(sides)
17 var previousSectorIn = true
18 for i in 0..<sides {
19 let segmentAngle = sectorAngle * Double.random(in: 0.7...1.3)
20 let angle = (sectorAngle * Double(i-0)) + segmentAngle
21 let radius = r * Double.random(in: 0.45...0.85)
22 let pt = Cartesian(length: radius, angle: angle)
23
24 let ctlAngle1 = angle - (segmentAngle * 0.75)
25 let ctlDistance1 = previousSectorIn ? radius*1.45 : radius*0.55
26 let ctl1 = Cartesian(length: ctlDistance1, angle: ctlAngle1)
27
28 let ctlAngle2 = angle - (segmentAngle * 0.25)
29 let ctlDistance2 = radius * Double.random(in: 0.55...1.45)
30 previousSectorIn = ctlDistance2 < radius
31 let ctl2 = Cartesian(length: ctlDistance2, angle: ctlAngle2)
32
33 let s:CubicSegment = CubicSegment(
34 point: CGPoint(x: pt.x + c.x, y: pt.y + c.y),
35 control1: CGPoint(x: ctl1.x + c.x, y: ctl1.y + c.y),
36 control2: CGPoint(x: ctl2.x + c.x, y: ctl2.y + c.y))
37 segments.append(s)
38 }
39 segments.append(segments[0])
40 return segments
41}
A Random shape is created from the array of CubicSegments with the size adjusted to fit
into the containing frame. This conforms to the Shape protocol.
1struct RandomShape: Shape {
2 var segments:[CubicSegment]
3
4 func path(in rect: CGRect) -> Path {
5 func adjustPoint(p: CGPoint) -> CGPoint {
6 return CGPoint(x: p.x * rect.width, y: p.y * rect.height)
7 }
8
9 var path = Path()
10 path.move(to: adjustPoint(p: segments[0].point))
11 for i in 1..<segments.count {
12 path.addCurve(to: adjustPoint(p: segments[i].point),
13 control1: adjustPoint(p: segments[i].control1),
14 control2: adjustPoint(p: segments[i].control2))
15 }
16 path.closeSubpath()
17 return path
18 }
19}
Two variables of RandomShape are created and these shapes are swapped when the
"Change" button is selected. Some attributes are animated such as color, but the
actual shape change is not animated. This is because the SwiftUI framework does not
know how to animate the transition from one list of CubicSegment to another.
1struct ChangeShapeView: View {
2 @State private var changeShape = true
3
4 let segmentsShape1 = CreateRandomShape(sides: 5)
5 let segmentsShape2 = CreateRandomShape(sides: 5)
6
7 var body: some View {
8 VStack {
9 RandomShape(segments: changeShape ? segmentsShape1 : segmentsShape2)
10 .stroke(changeShape ? Color.purple : .red, lineWidth: 6.0)
11 .frame(width: 200, height: 200)
12 .animation(.easeInOut(duration: 2))
13
14 RandomShape(segments: changeShape ? segmentsShape1 : segmentsShape2)
15 .fill(changeShape ? Color.purple : .red)
16 .frame(width: 200, height: 200)
17 .animation(.linear(duration: 2))
18
19 Button("Change") {
20 self.changeShape.toggle()
21 }
22 .buttonStyle(BlueButtonStyle())
23
24 Spacer()
25 }
26 }
27}
Random shape created with array of cubic curves
Use array of Animatable Cubic Curve
An AnimatableCubicCurve was defined in How to animate a Cubic Curve change in
SwiftUI and these were combined in a view in a ZStack to create a shape. Each of
these curves is Animatable, so could an array of these curves be used to define a
shape and allow animation of a shape change? The short answer is no, because even if
the individual segments are animatable, the shape of an array is not animatable. In
order to animate a shape change, the SwiftUI framework needs to be able to calculate
intermediate stage in the transition.
1struct AnimatableCubicCurve : VectorArithmetic {
2 var start: CGPoint
3 var end: CGPoint
4 var control1: CGPoint
5 var control2: CGPoint
6
7 var length: Double {
8 return Double(((end.x - start.x) * (end.x - start.x)) +
9 ((end.y - start.y) * (end.y - start.y))).squareRoot()
10 }
11
12 var magnitudeSquared: Double {
13 return length * length
14 }
15
16 mutating func scale(by rhs: Double) {
17 self.start.x.scale(by: rhs)
18 self.start.y.scale(by: rhs)
19 self.end.x.scale(by: rhs)
20 self.end.y.scale(by: rhs)
21 self.control1.x.scale(by: rhs)
22 self.control1.y.scale(by: rhs)
23 self.control2.x.scale(by: rhs)
24 self.control2.y.scale(by: rhs)
25 }
26
27 static var zero: AnimatableCubicCurve {
28 return AnimatableCubicCurve(start: CGPoint(x: 0.0, y: 0.0),
29 end: CGPoint(x: 0.0, y: 0.0),
30 control1: CGPoint(x: 0.0, y: 0.0),
31 control2: CGPoint(x: 0.0, y: 0.0))
32 }
33
34 static func - (lhs: AnimatableCubicCurve, rhs: AnimatableCubicCurve) -> AnimatableCubicCurve {
35 return AnimatableCubicCurve(
36 start: CGPoint(
37 x: lhs.start.x - rhs.start.x,
38 y: lhs.start.y - rhs.start.y),
39 end: CGPoint(
40 x: lhs.end.x - rhs.end.x,
41 y: lhs.end.y - rhs.end.y),
42 control1: CGPoint(
43 x: lhs.control1.x - rhs.control1.x,
44 y: lhs.control1.y - rhs.control1.y),
45 control2: CGPoint(
46 x: lhs.control2.x - rhs.control2.x,
47 y: lhs.control2.y - rhs.control2.y))
48 }
49
50 static func -= (lhs: inout AnimatableCubicCurve, rhs: AnimatableCubicCurve) {
51 lhs = lhs - rhs
52 }
53
54 static func + (lhs: AnimatableCubicCurve, rhs: AnimatableCubicCurve) -> AnimatableCubicCurve {
55 return AnimatableCubicCurve(
56 start: CGPoint(
57 x: lhs.start.x + rhs.start.x,
58 y: lhs.start.y + rhs.start.y),
59 end: CGPoint(
60 x: lhs.end.x + rhs.end.x,
61 y: lhs.end.y + rhs.end.y),
62 control1: CGPoint(
63 x: lhs.control1.x + rhs.control1.x,
64 y: lhs.control1.y + rhs.control1.y),
65 control2: CGPoint(
66 x: lhs.control2.x + rhs.control2.x,
67 y: lhs.control2.y + rhs.control2.y))
68 }
69
70 static func += (lhs: inout AnimatableCubicCurve, rhs: AnimatableCubicCurve) {
71 lhs = lhs + rhs
72 }
73
74 static func * (lhs: AnimatableCubicCurve, rhs: Double) -> AnimatableCubicCurve {
75 return AnimatableCubicCurve(
76 start: CGPoint(
77 x: lhs.start.x * CGFloat(rhs),
78 y: lhs.start.y * CGFloat(rhs)),
79 end: CGPoint(
80 x: lhs.end.x * CGFloat(rhs),
81 y: lhs.end.y * CGFloat(rhs)),
82 control1: CGPoint(
83 x: lhs.control1.x * CGFloat(rhs),
84 y: lhs.control1.y * CGFloat(rhs)),
85 control2: CGPoint(
86 x: lhs.control2.x * CGFloat(rhs),
87 y: lhs.control2.y * CGFloat(rhs)))
88 }
89}
1struct CubicCurveShape: Shape {
2 var startPoint: CGPoint
3 var endPoint: CGPoint
4 var controlPoint1: CGPoint
5 var controlPoint2: CGPoint
6
7 private var animatableSegment: AnimatableCubicCurve
8
9 var animatableData: AnimatableCubicCurve {
10 get { AnimatableCubicCurve(
11 start: startPoint, end: endPoint, control1: controlPoint1, control2: controlPoint2) }
12 set {
13 startPoint = newValue.start
14 endPoint = newValue.end
15 controlPoint1 = newValue.control1
16 controlPoint2 = newValue.control2
17 }
18 }
19
20 init(startPoint: CGPoint, endPoint: CGPoint, controlPoint1: CGPoint, controlPoint2: CGPoint) {
21 self.startPoint = startPoint
22 self.endPoint = endPoint
23 self.controlPoint1 = controlPoint1
24 self.controlPoint2 = controlPoint2
25 self.animatableSegment = AnimatableCubicCurve(
26 start: startPoint,
27 end: endPoint,
28 control1: controlPoint1,
29 control2: controlPoint2)
30 }
31
32 init(curve: AnimatableCubicCurve) {
33 self.init(startPoint: curve.start,
34 endPoint: curve.end,
35 controlPoint1: curve.control1,
36 controlPoint2: curve.control2)
37 }
38
39 func path(in rect: CGRect) -> Path {
40 let start = CGPoint(x: startPoint.x * rect.width,
41 y: startPoint.y * rect.height)
42 let end = CGPoint(x: rect.width * endPoint.x,
43 y: rect.height * endPoint.y)
44 let control1 = CGPoint(x: rect.width * controlPoint1.x,
45 y: rect.height * controlPoint1.y)
46 let control2 = CGPoint(x: rect.width * controlPoint2.x,
47 y: rect.height * controlPoint2.y)
48
49 var path = Path()
50 path.move(to: start)
51 path.addCurve(to: end, control1: control1, control2: control2)
52 return path
53 }
54}
1func CreateRandomShape2(segments:Int) -> [AnimatableCubicCurve] {
2 var curves:[AnimatableCubicCurve] = []
3
4 let r = 0.5
5 let c = CGPoint(x: 0.5, y: 0.5)
6 let sectorAngle = 2.0 * Double.pi / Double(segments)
7 var previousSectorIn = true
8 var previousPoint = CGPoint(x: 0.0, y: 0.0)
9 for i in 0..<segments {
10 let segmentAngle = sectorAngle * Double.random(in: 0.7...1.3)
11 let angle = (sectorAngle * Double(i-0)) + segmentAngle
12 let radius = r * Double.random(in: 0.45...0.85)
13 let pt = Cartesian(length: radius, angle: angle)
14
15 let ctlAngle1 = angle - (segmentAngle * 0.75)
16 let ctlDistance1 = previousSectorIn ? radius*1.45 : radius*0.55
17 let ctl1 = Cartesian(length: ctlDistance1, angle: ctlAngle1)
18
19 let ctlAngle2 = angle - (segmentAngle * 0.25)
20 let ctlDistance2 = radius * Double.random(in: 0.55...1.45)
21 previousSectorIn = ctlDistance2 < radius
22 let ctl2 = Cartesian(length: ctlDistance2, angle: ctlAngle2)
23
24 let curve: AnimatableCubicCurve = AnimatableCubicCurve (
25 start: previousPoint,
26 end: CGPoint(x: pt.x + c.x, y: pt.y + c.y),
27 control1: CGPoint(x: ctl1.x + c.x, y: ctl1.y + c.y),
28 control2: CGPoint(x: ctl2.x + c.x, y: ctl2.y + c.y))
29 curves.append(curve)
30 previousPoint = curve.end
31 }
32 curves.append(curves[0])
33 return curves
34}
1struct ShapeWithCubicCurveView: View {
2 @State private var changeShape = true
3
4 let segmentsShape1 = CreateRandomShape2(segments: 8)
5 let segmentsShape2 = CreateRandomShape2(segments: 8)
6
7 var body: some View {
8 VStack {
9 RandomShape2(segments: changeShape ? segmentsShape1 : segmentsShape2)
10 .stroke(changeShape ? Color.purple : .red, lineWidth: 6.0)
11 .frame(width: 200, height: 200)
12 .animation(.easeInOut(duration: 2))
13
14 RandomShape2(segments: changeShape ? segmentsShape1 : segmentsShape2)
15 .fill(changeShape ? Color.purple : .red)
16 .frame(width: 200, height: 200)
17 .animation(.linear(duration: 2))
18
19 Button("Change") {
20 self.changeShape.toggle()
21 }
22 .buttonStyle(BlueButtonStyle())
23
24 Spacer()
25 }
26 }
27}
Random shape created with array of animatable curves
Animate an array of values
Previous shapes were animated by implementing Animatable protocol and supplying the AnimatableData. The AnimatableData has either been a single value or a number of values representing a single point or curve. Now we want to animate a series of values and the number of values in the series is open ended.
First animate a line that is composed of a list of doubles for it's "y" coordinates,
while the "x" coordinates are distributed horizontally across the containing frame.
The AnimatableLine structure is defined to contain the array of doubles and to
conform to VectorArithmetic protocol. This is used as the AnimatableData for
the LineShape shape.
This shows that it is possible to animate the transition from one set of values to another once the AnimatableData structure conforms to VectorArithmetic. This code will only work well with arrays that have the same number of samples. We'll deal with arrays of unequal length later when we deal with arrays of cubic curves.
1struct AnimatableLine : VectorArithmetic {
2 var values:[Double]
3
4 var magnitudeSquared: Double {
5 return values.map{ $0 * $0 }.reduce(0, +)
6 }
7
8 mutating func scale(by rhs: Double) {
9 values = values.map{ $0 * rhs }
10 }
11
12 static var zero: AnimatableLine {
13 return AnimatableLine(values: [0.0])
14 }
15
16 static func - (lhs: AnimatableLine, rhs: AnimatableLine) -> AnimatableLine {
17 return AnimatableLine(values: zip(lhs.values, rhs.values).map(-))
18 }
19
20 static func -= (lhs: inout AnimatableLine, rhs: AnimatableLine) {
21 lhs = lhs - rhs
22 }
23
24 static func + (lhs: AnimatableLine, rhs: AnimatableLine) -> AnimatableLine {
25 return AnimatableLine(values: zip(lhs.values, rhs.values).map(+))
26 }
27
28 static func += (lhs: inout AnimatableLine, rhs: AnimatableLine) {
29 lhs = lhs + rhs
30 }
31}
1struct LineShape: Shape {
2 var yValues: [Double]
3
4 var animatableData: AnimatableLine {
5 get { AnimatableLine(values: yValues) }
6 set { yValues = newValue.values }
7 }
8
9 func path(in rect: CGRect) -> Path {
10 let xIncrement = (rect.width / CGFloat(yValues.count))
11 var path = Path()
12 path.move(to: CGPoint(x: 0.0, y: yValues[0] * Double(rect.width)))
13 for i in 1..<yValues.count {
14 let pt = CGPoint(x: (Double(i) * Double(xIncrement)), y: (yValues[i] * Double(rect.height)))
15 path.addLine(to: pt)
16 }
17 return path
18 }
19}
1struct LineView: View {
2 @State private var changeShape = true
3
4 let line1 = [0.2, 0.4, 0.2, 0.8, 0.9, 0.1]
5 let line2 = [0.3, 0.9, 0.9, 0.8, 0.2, 0.5]
6
7 var body: some View {
8 VStack {
9 Text("Animated Line")
10
11 LineShape(yValues: changeShape ? line1 : line2)
12 .stroke(changeShape ? Color.blue : .red, lineWidth: 4.0)
13 .frame(width: 350, height: 420)
14 .animation(.easeInOut(duration: 2))
15
16 Button("Change") {
17 self.changeShape.toggle()
18 }
19 .buttonStyle(BlueButtonStyle())
20
21 Spacer()
22 }
23 }
24}

Animate line change with an array of doubles
Animate between shapes with the same number of sections
We started with a list of doubles for an animatable line to demonstrate specifying
AnimatableData with a list of values. We can build on this by first defining a struct
CubicCurve to contain the three points required for a Cubic Bézier curve that
conforms to VectorArithmetic.
1struct CubicCurve : VectorArithmetic {
2 var point: CGPoint
3 var control1: CGPoint
4 var control2: CGPoint
5
6 var magnitudeSquared: Double {
7 return 0.0
8 }
9
10 mutating func scale(by rhs: Double) {
11 self.point.x.scale(by: rhs)
12 self.point.y.scale(by: rhs)
13 self.control1.x.scale(by: rhs)
14 self.control1.y.scale(by: rhs)
15 self.control2.x.scale(by: rhs)
16 self.control2.y.scale(by: rhs)
17 }
18
19 static var zero: CubicCurve {
20 return CubicCurve(point: CGPoint(x: 0.0, y: 0.0),
21 control1: CGPoint(x: 0.0, y: 0.0),
22 control2: CGPoint(x: 0.0, y: 0.0))
23 }
24
25 static func - (lhs: CubicCurve, rhs: CubicCurve) -> CubicCurve {
26 return CubicCurve(
27 point: CGPoint(
28 x: lhs.point.x - rhs.point.x,
29 y: lhs.point.y - rhs.point.y),
30 control1: CGPoint(
31 x: lhs.control1.x - rhs.control1.x,
32 y: lhs.control1.y - rhs.control1.y),
33 control2: CGPoint(
34 x: lhs.control2.x - rhs.control2.x,
35 y: lhs.control2.y - rhs.control2.y))
36 }
37
38 static func -= (lhs: inout CubicCurve, rhs: CubicCurve) {
39 lhs = lhs - rhs
40 }
41
42 static func + (lhs: CubicCurve, rhs: CubicCurve) -> CubicCurve {
43 return CubicCurve(
44 point: CGPoint(
45 x: lhs.point.x + rhs.point.x,
46 y: lhs.point.y + rhs.point.y),
47 control1: CGPoint(
48 x: lhs.control1.x + rhs.control1.x,
49 y: lhs.control1.y + rhs.control1.y),
50 control2: CGPoint(
51 x: lhs.control2.x + rhs.control2.x,
52 y: lhs.control2.y + rhs.control2.y))
53 }
54
55 static func += (lhs: inout CubicCurve, rhs: CubicCurve) {
56 lhs = lhs + rhs
57 }
58
59 static func * (lhs: CubicCurve, rhs: Double) -> CubicCurve {
60 return CubicCurve(
61 point: CGPoint(
62 x: lhs.point.x * CGFloat(rhs),
63 y: lhs.point.y * CGFloat(rhs)),
64 control1: CGPoint(
65 x: lhs.control1.x * CGFloat(rhs),
66 y: lhs.control1.y * CGFloat(rhs)),
67 control2: CGPoint(
68 x: lhs.control2.x * CGFloat(rhs),
69 y: lhs.control2.y * CGFloat(rhs)))
70 }
71}
Next define a struct AnimatableCubicCurveList that contains a list of these
CubicCurve and also conforms to VectorArithmetic. We ignore dot product here
and return zero for magnitudeSquared. In vector math, doProduct is commonly used to
determine how aligned two vectors are and this is not appropriate for a list of cubic
curves. This does not appear to be used for basic shape animation.
1struct AnimatableCubicCurveList : VectorArithmetic {
2 var values:[CubicCurve]
3
4 var magnitudeSquared: Double {
5 // dotProduct has no meaning on a list of cubic curves
6 return 0.0
7 }
8
9 mutating func scale(by rhs: Double) {
10 values = values.map { $0 * rhs }
11 }
12
13 static var zero: AnimatableCubicCurveList {
14 return AnimatableCubicCurveList(values: [CubicCurve.zero])
15 }
16
17 static func - (lhs: AnimatableCubicCurveList, rhs: AnimatableCubicCurveList) ->
18 AnimatableCubicCurveList {
19 let result = zip(lhs.values, rhs.values).map(-)
20 return AnimatableCubicCurveList(values: result)
21 }
22
23 static func -= (lhs: inout AnimatableCubicCurveList, rhs: AnimatableCubicCurveList) {
24 lhs = lhs - rhs
25 }
26
27 static func + (lhs: AnimatableCubicCurveList, rhs: AnimatableCubicCurveList) ->
28 AnimatableCubicCurveList {
29 let result = zip(lhs.values, rhs.values).map(+)
30 return AnimatableCubicCurveList(values: result)
31 }
32
33 static func += (lhs: inout AnimatableCubicCurveList, rhs: AnimatableCubicCurveList) {
34 lhs = lhs + rhs
35 }
36}
1struct AnimatableShape: Shape {
2 var curves:[CubicCurve]
3
4 var animatableData: AnimatableCubicCurveList {
5 get { AnimatableCubicCurveList(values: curves) }
6 set { curves = newValue.values }
7 }
8
9 func path(in rect: CGRect) -> Path {
10 func adjustPoint(p: CGPoint) -> CGPoint {
11 return CGPoint(x: p.x * rect.width, y: p.y * rect.height)
12 }
13
14 var path = Path()
15 path.move(to: adjustPoint(p: curves[0].point))
16 for i in 1..<curves.count {
17 path.addCurve(to: adjustPoint(p: curves[i].point),
18 control1: adjustPoint(p: curves[i].control1),
19 control2: adjustPoint(p: curves[i].control2))
20 }
21 path.closeSubpath()
22 return path
23 }
24}
A helper function is defined to generate a random shape consisting of an array of
CubicCurves. Note that the first point is appended to the end of the array as the
point in this curve is first used to move the path to this point. This same point at
the end of the path is used to define the cubic curve back to the starting point.
1func CreateRandomShape3(segments:Int) -> [CubicCurve] {
2 var curves:[CubicCurve] = []
3
4 let r = 0.5
5 let c = CGPoint(x: 0.5, y: 0.5)
6 let sectorAngle = 2.0 * Double.pi / Double(segments)
7 var previousSectorIn = true
8 for i in 0..<segments {
9 let segmentAngle = sectorAngle * Double.random(in: 0.7...1.3)
10 let angle = (sectorAngle * Double(i-0)) + segmentAngle
11 let radius = r * Double.random(in: 0.45...0.85)
12 let pt = Cartesian(length: radius, angle: angle)
13
14 let ctlAngle1 = angle - (segmentAngle * 0.75)
15 let ctlDistance1 = previousSectorIn ? radius*1.45 : radius*0.55
16 let ctl1 = Cartesian(length: ctlDistance1, angle: ctlAngle1)
17
18 let ctlAngle2 = angle - (segmentAngle * 0.25)
19 let ctlDistance2 = radius * Double.random(in: 0.55...1.45)
20 previousSectorIn = ctlDistance2 < radius
21 let ctl2 = Cartesian(length: ctlDistance2, angle: ctlAngle2)
22
23 let curve = CubicCurve (
24 point: CGPoint(x: pt.x + c.x, y: pt.y + c.y),
25 control1: CGPoint(x: ctl1.x + c.x, y: ctl1.y + c.y),
26 control2: CGPoint(x: ctl2.x + c.x, y: ctl2.y + c.y))
27 curves.append(curve)
28 }
29 curves.append(curves[0])
30
31 return curves
32}
This shape now demonstrates a smooth animation from one shape to another.
1struct AnimatableShapeView: View {
2 @State private var changeShape = true
3
4 let shape1 = CreateRandomShape3(segments: 19)
5 let shape2 = CreateRandomShape3(segments: 19)
6
7 var body: some View {
8 VStack {
9 Text("Shape Change - Equal Segments")
10
11 AnimatableShape(curves: changeShape ? shape1 : shape2)
12 .stroke(changeShape ? Color.purple : .red, lineWidth: 3.0)
13 .frame(width: 200, height: 200)
14 .animation(.easeInOut(duration: 2))
15
16 AnimatableShape(curves: changeShape ? shape1 : shape2)
17 .fill(changeShape ? Color.green : .yellow)
18 .frame(width: 200, height: 200)
19 .animation(.easeInOut(duration: 2))
20
21 Button("Change") {
22 self.changeShape.toggle()
23 }
24 .buttonStyle(BlueButtonStyle())
25
26 Spacer()
27 }
28 }
29}
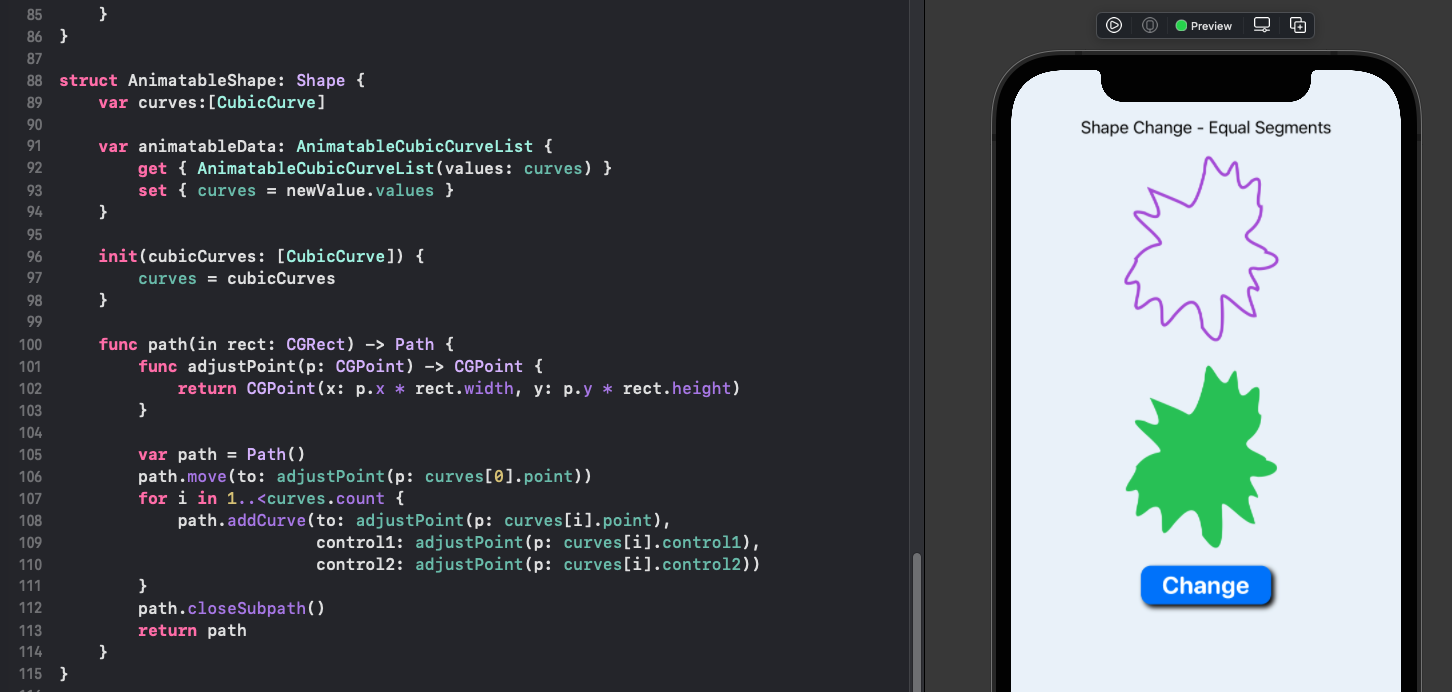

Animate shape change when shapes have equal number of segments
Animate between shapes of different number of segments
The above AnimatableShape works well when the number of Cubic Curves in the shapes
to change are the same. However, when there is a difference in the number of curves
the animation only works where the number of curves overlap. When switching from the
larger one to the smaller one, the extra curves are first removed and then the
remaining part of the shape is animated. Similarly, when transitioning to the larger
one, the smaller shape is first animated and then the extra section just appears.
1struct UnequalSegmentsView: View {
2 @State private var changeShape = true
3
4 let shape1 = CreateRandomShape3(segments: 8)
5 let shape2 = CreateRandomShape3(segments: 12)
6
7 var body: some View {
8 VStack {
9 Text("Shape Change - Unequal Segments")
10
11 AnimatableShape(curves: changeShape ? shape1 : shape2)
12 .stroke(changeShape ? Color.blue : .red, lineWidth: 3.0)
13 .frame(width: 200, height: 200)
14 .animation(.easeInOut(duration: 2))
15
16 AnimatableShape(curves: changeShape ? shape1 : shape2)
17 .fill(changeShape ? Color.green : .yellow)
18 .frame(width: 200, height: 200)
19 .animation(.easeInOut(duration: 2))
20
21 Button("Change") {
22 self.changeShape.toggle()
23 }
24 .buttonStyle(BlueButtonStyle())
25
26 Spacer()
27 }
28 }
29}
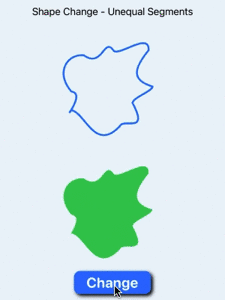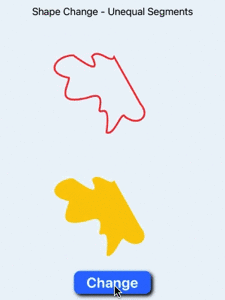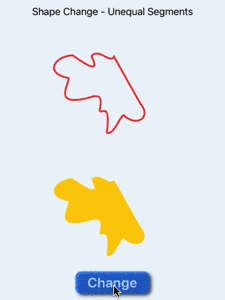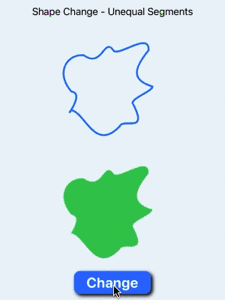
Animate shape change when shapes have unequal number of segments
Improving animation of shape with different number of segments
We need to change the + and - functions on the AnimatableCubicCurveList to
address the smooth animation between shapes with different numbers of curves.
Essentially, we need to add curves to the shorter list so that the two shapes contain
the same number of curves. Two helper functions are added in
AnimatableCubicCurveList2; equalizeArrays is a function to ensure the two arrays
are of equal size and this is used in both the + and - functions;
padShorterList functions is called by equalizeArrays and creates a curve matching
all three points in the curve with the first point of the shorter array and adding
repeats of this to the end of the array until the sizes match. This will have the
effect of collapsing all the extra curves in the larger shape onto the first/last
point of the smaller shape during the transition. The new curves for the larger shape
will animate from the start point of the smaller shape.
1struct AnimatableCubicCurveList2 : VectorArithmetic {
2 var values:[CubicCurve]
3
4 var magnitudeSquared: Double {
5 // dotProduct has no meaning on a list of cubic curves
6 return 0.0
7 }
8
9 mutating func scale(by rhs: Double) {
10 values = values.map { $0 * rhs }
11 }
12
13 static var zero: AnimatableCubicCurveList2 {
14 return AnimatableCubicCurveList2(values: [CubicCurve.zero])
15 }
16
17 fileprivate static func padShorterList(_ shortList: inout [CubicCurve], _ longList: [CubicCurve]) {
18 // Create a curve with all points set to the first/last point
19 // Extend the shorter list with repeats of this point
20 let point = shortList[0].point
21 let curve = CubicCurve(point: point, control1: point, control2: point)
22 for _ in(shortList.count..<longList.count) {
23 shortList.append(curve)
24 }
25 }
26
27 fileprivate static func equalizeArrays(_ lhs: AnimatableCubicCurveList2, _ rhs: AnimatableCubicCurveList2) -> ([CubicCurve], [CubicCurve]) {
28 var leftValues = lhs.values
29 var rightValues = rhs.values
30 if leftValues.count < rightValues.count {
31 padShorterList(&leftValues, rightValues)
32 }
33 else if rightValues.count < leftValues.count {
34 padShorterList(&rightValues, leftValues)
35 }
36 return (leftValues, rightValues)
37 }
38
39 static func - (lhs: AnimatableCubicCurveList2, rhs: AnimatableCubicCurveList2) -> AnimatableCubicCurveList2 {
40 // Ensure the shapes have the same number of curves
41 let lists = equalizeArrays(lhs, rhs)
42 let result = zip(lists.0, lists.1).map(-)
43 return AnimatableCubicCurveList2(values: result)
44 }
45
46 static func -= (lhs: inout AnimatableCubicCurveList2, rhs: AnimatableCubicCurveList2) {
47 lhs = lhs - rhs
48 }
49
50 static func + (lhs: AnimatableCubicCurveList2, rhs: AnimatableCubicCurveList2) -> AnimatableCubicCurveList2 {
51 // Ensure the shapes have the same number of curves
52 let lists = equalizeArrays(lhs, rhs)
53 let result = zip(lists.0, lists.1).map(+)
54 return AnimatableCubicCurveList2(values: result)
55 }
56
57 static func += (lhs: inout AnimatableCubicCurveList2, rhs: AnimatableCubicCurveList2) {
58 lhs = lhs + rhs
59 }
60}
1struct AnimatableShape2: Shape {
2 var curves:[CubicCurve]
3
4 var animatableData: AnimatableCubicCurveList3 {
5 get { AnimatableCubicCurveList3(values: curves) }
6 set { curves = newValue.values }
7 }
8
9 func path(in rect: CGRect) -> Path {
10 func adjustPoint(p: CGPoint) -> CGPoint {
11 return CGPoint(x: p.x * rect.width, y: p.y * rect.height)
12 }
13
14 var path = Path()
15 path.move(to: adjustPoint(p: curves[0].point))
16 for i in 1..<curves.count {
17 path.addCurve(to: adjustPoint(p: curves[i].point),
18 control1: adjustPoint(p: curves[i].control1),
19 control2: adjustPoint(p: curves[i].control2))
20 }
21 path.closeSubpath()
22 return path
23 }
24}
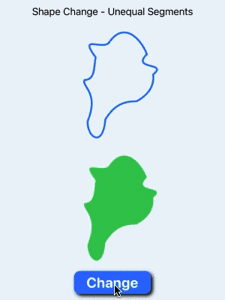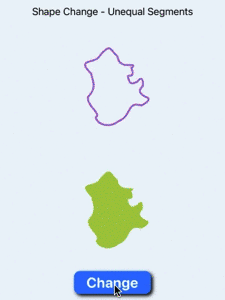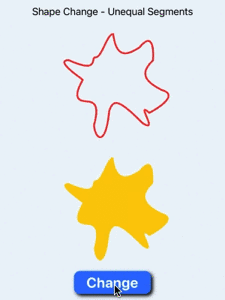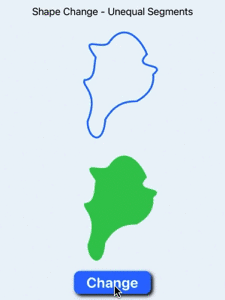
Smooth animation of shape change when shapes have unequal numbers of segments
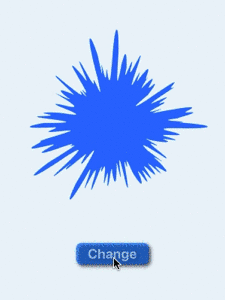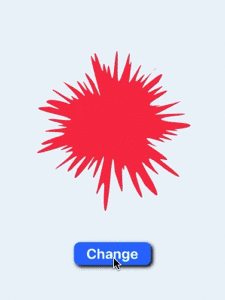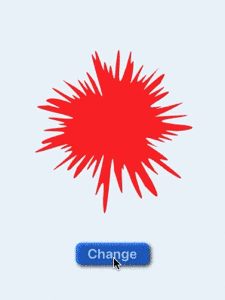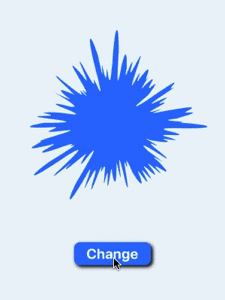
Animation random shape change with many segments
Conclusion
This article built on the previous articles on animating various paths. Animation of a shape is dependent on providing the SwiftUI framework with information to calculate intermediate states. This is done by defining the AnimatableData for the custom shape so that SwiftUI can present a smooth transition from one shape to another.
In a previous article, an array of AnimatableCubicCurve were arranged in a ZStack
to present a shape. This provided a good outline of a shape, but cannot be used as a
shape, such as the fill modifier cannot be applied. The AnimatableShape2 defined in
this article defines a random shape composed of a number of cubic Bézier curves and
is a true shape. It allows for smooth animation between different random shapes as
well as scaling and color change.