Integer division of negative numbers
It may be surprising that there is a difference in integer division between Python and other languages like Swift, C++ and Java when it comes to negative numbers.
The reason for this difference is because "Integer division" is not a well-defined concept and the specification for each language can choose truncation towards zero or negative infinity as its defined result for the operation. Guido van Rossum wrote a post on the reasoning behind the decision in Python - Why Python's Integer Division Floors
Division and Integer Division
The following example shows that integer division between two numbers does not yield the same absolute value when one of the numbers is negative. The results show that the float division is identical except for the negative sign, while the integer division results are different.
1for i in range(1,12):
2 print(f"{11//i}, {-11//i}, {11/i:.2F} {-11/i:.2F}")
Comparison of integer division with positive and negative numbers in Python
| i | 11 // i | -11 // i | 11 / i | -11 / i |
|---|---|---|---|---|
| 1 | 11 | -11 | 11.00 | -11.00 |
| 2 | 5 | -6 | 5.50 | -5.50 |
| 3 | 3 | -4 | 3.67 | -3.67 |
| 4 | 2 | -3 | 2.75 | -2.75 |
| 5 | 2 | -3 | 2.20 | -2.20 |
| 6 | 1 | -2 | 1.83 | -1.83 |
| 7 | 1 | -2 | 1.57 | -1.57 |
| 8 | 1 | -2 | 1.38 | -1.38 |
| 9 | 1 | -2 | 1.22 | -1.22 |
| 10 | 1 | -2 | 1.10 | -1.10 |
| 11 | 1 | -1 | 1.00 | -1.00 |
Division and Integer Division results in Swift
Similar code run in Swift yields different results. These match the results for C++.
1for i in 1...11{
2 print("\(i) : \(11/i), \(-11/i), \(11.0/Double(i)), \(-11.0/Double(i))")
3}
Comparison of integer division with positive and negative numbers in Swift
| i | 11 // i | -11 // i | 11 / i | -11 / i |
|---|---|---|---|---|
| 1 | 11 | -11 | 11.00 | -11.00 |
| 2 | 5 | -5 | 5.50 | -5.50 |
| 3 | 3 | -3 | 3.67 | -3.67 |
| 4 | 2 | -2 | 2.75 | -2.75 |
| 5 | 2 | -2 | 2.20 | -2.20 |
| 6 | 1 | -1 | 1.83 | -1.83 |
| 7 | 1 | -1 | 1.57 | -1.57 |
| 8 | 1 | -1 | 1.38 | -1.38 |
| 9 | 1 | -1 | 1.22 | -1.22 |
| 10 | 1 | -1 | 1.10 | -1.10 |
| 11 | 1 | -1 | 1.00 | -1.00 |
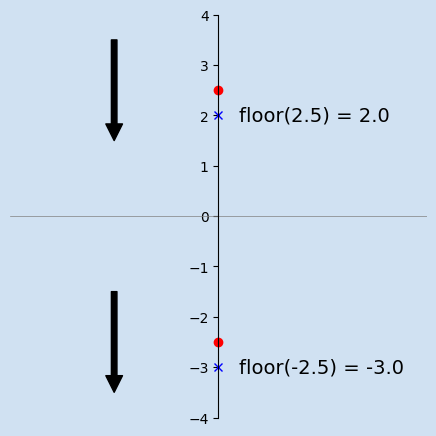
Floor
Take a specific example from above such as 11//4 that results in a value
of 2.75. It is easy to assume, when dealing with positive numbers, that the
digits after the decimal point are discarded and the integer value returned is the number
before the decimal point. This is true for positive numbers, but the same assumption
for negative numbers would suggest a result of -2, which is incorrect for
Python. Python uses math.floor to determine the integer result and math.floor returns
the next integer value towards negative infinity. Other languages truncate the value
towards zero and thus return a different result.
It is shown below that both the positive and negative result is ±2.75, but the positive integer result is 2 and the negative integer result is -3.
1print(11//4)
2"""
32
4"""
5
6print(11//-4)
7"""
8-3
9"""
10
11print(11/4)
12"""
132.75
14"""
15
16print(11/-4)
17"""
18-2.75
19"""
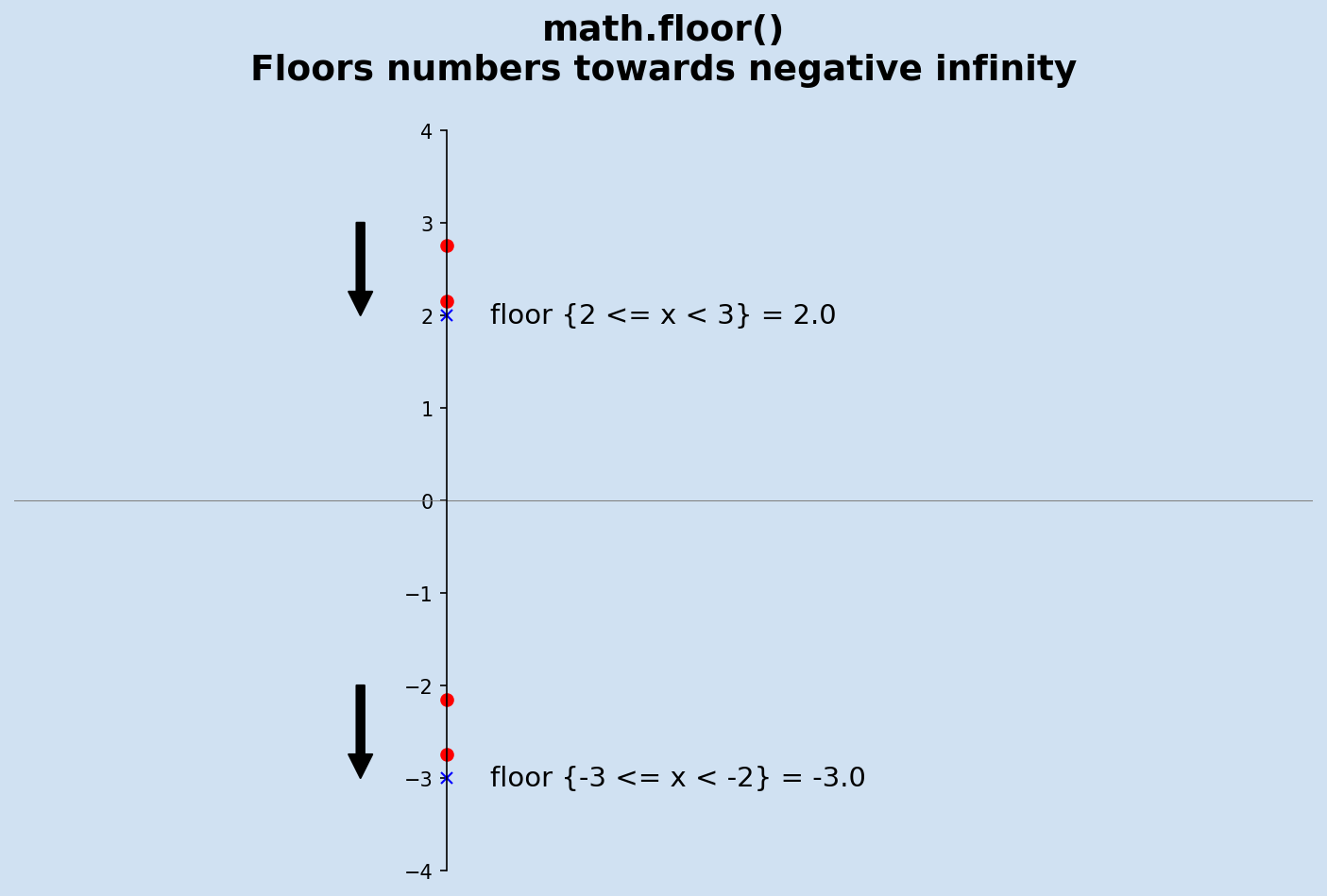
math.floor truncates towards negative infinity
Other math functions
It should be noted that converting a double to an integer in Python does truncate
towards zero. Rounding a double number with math.round returns the corresponding
positive or negative nearest absolute whole number. math.trunc truncates the
number towards zero, but math.floor floors towards negative infinity.
1int(2.75), int(-2.75), int(2.15), int(-2.15)
2"""
3(2, -2, 2, -2)
4"""
5
6round(2.75), round(-2.75), round(2.15), round(-2.15)
7"""
8(3, -3, 2, -2)
9"""
10
11math.floor(2.75), math.floor(-2.75), math.floor(2.15), math.floor(-2.15)
12"""
13(2, -3, 2, -3)
14"""
15
16math.trunc(2.75), math.trunc(-2.75), math.trunc(2.15), math.trunc(-2.15)
17"""
18(2, -2, 2, -2)
19"""

Conclusion
In Python integer division on negative numbers produces different absolute values than the equivalent integer division on positive numbers. The behavior is consistent within the language and the reason is the use of floor of the result rather than truncation. This may come to light from time to time when adopting an algorithm from on e language to another and discovering discrepancies. If in doubt, test the results of integer division with negative numbers in the language or avoid integer division when dealing with negative numbers.